ორმაგი ინტეგრალის განმარტება. ორმაგი ინტეგრალი

ორმაგი ინტეგრალის თვისებები.

ორმაგი ინტეგრალის ზოგიერთი თვისება პირდაპირ გამომდინარეობს ამ კონცეფციის განმარტებიდან და ინტეგრალური ჯამების თვისებებიდან, კერძოდ:

1. თუ ფუნქცია f(x, y)აერთიანებს დ, ეს kf (x, y)ასევე ინტეგრირებადია ამ რეგიონში და (24.4)

2. თუ ტერიტორიაზე დინტეგრირებადი ფუნქციები f(x, y)და g (x, y), შემდეგ ამ დომენში ფუნქციები f(x, y) ± g(x, y)და სადაც

3. თუ იმ ტერიტორიაზე ინტეგრირებულთათვის დფუნქციები f(x, y)და g (x, y)უთანასწორობა მოქმედებს f(x, y)≤g (x, y), ეს

(24.6)

მოდით დავამტკიცოთ ორმაგი ინტეგრალის კიდევ რამდენიმე თვისება:

4. თუ ფართობი დდაყოფილია ორ ზონად დ 1 და დ 2 საერთო შიდა წერტილებისა და ფუნქციის გარეშე f(x, y)უწყვეტი რეგიონში დ, ეს

(24.7) მტკიცებულება . მთლიანი ჯამი ფართობზე დშეიძლება წარმოდგენილი იყოს როგორც:

სად არის ფართობის დანაყოფი დშედგენილია ისე, რომ საზღვარი შორის დ 1 და დ 2 შედგება დანაყოფის ნაწილების საზღვრებისგან. შემდეგ ზღვარზე გადასვლისას ვიღებთ ტოლობას (24.7).

5. ინტეგრალობის შემთხვევაში on დფუნქციები f(x, y)ამ დომენში ფუნქცია ასევე ინტეგრირებულია | f(x, y) |, და უთანასწორობა მოქმედებს

(24.8)

მტკიცებულება.

საიდანაც, ზღვარზე გადასვლის გამოყენებით, მივიღებთ უტოლობას (24.8)

6. სადაც ს დ- რეგიონის ტერიტორია დ.ამ განცხადების დადასტურებას ვიღებთ ინტეგრალური ჯამის ჩანაცვლებით f(x, y)≡ 0.

7. თუ ინტეგრირებულია ტერიტორიაზე დფუნქცია f(x, y)აკმაყოფილებს უთანასწორობას

m ≤ f(x, y) ≤ M,

რომ (24.9)

მტკიცებულება.

მტკიცებულება ხორციელდება აშკარა უთანასწორობის ზღვარზე გადასვლით

შედეგი.

თუ უტოლობის ყველა ნაწილს (24.9) გავყოფთ დჩვენ შეგვიძლია მივიღოთ ე.წ. საშუალო ღირებულების თეორემა:

კერძოდ, ფუნქციის უწყვეტობის პირობით ვვ დარის ასეთი წერტილი ამ რეგიონში ( x 0, y 0), სადაც ვ(x 0, y 0) = μ , ანუ

საშუალო მნიშვნელობის თეორემის კიდევ ერთი ფორმულირება.

ორმაგი ინტეგრალის გეომეტრიული მნიშვნელობა.

განიხილეთ სხეული ვ, შემოიფარგლება განტოლებით მოცემული ზედაპირის ნაწილით z = f (x, y),პროექტირება დეს ზედაპირი O სიბრტყემდე xyდა გვერდითი ცილინდრული ზედაპირი, მიღებული ვერტიკალური გენერატრიებიდან, რომლებიც აკავშირებენ ზედაპირის საზღვრის წერტილებს მათ პროექციებთან.

z=f(x,y)

ვ

წ P i Dნახ.2.

ჩვენ ვეძებთ ამ სხეულის მოცულობას, როგორც ცილინდრების მოცულობის ჯამის ზღვარს, რომელთა ფუძეები არის Δ ნაწილები. ს ირეგიონი დდა სიმაღლეები სიგრძის სეგმენტებია ვ(P i), სადაც პუნქტები P iეკუთვნის Δ ს ი. ლიმიტზე გადასვლისას ვიღებთ ამას

(24.11)

ანუ ორმაგი ინტეგრალი წარმოადგენს ეგრეთ წოდებული ცილინდეროიდის მოცულობას, რომელიც ზემოდან შემოიფარგლება ზედაპირით z = f(x, y), ხოლო ქვემოთ – რეგიონი დ.

ორმაგი ინტეგრალის გამოთვლა მისი განმეორებით შემცირებით.

განიხილეთ ტერიტორია დ, შემოსაზღვრული ხაზებით x = a, x = b(ა< b ), სადაც φ 1 ( X) და φ 2 ( X) უწყვეტია [ ა, ბ]. შემდეგ ნებისმიერი სწორი ხაზი კოორდინატთა ღერძის O-ს პარალელურად ზედა გადის რეგიონის შიდა წერტილში დკვეთს რეგიონის საზღვარს ორ წერტილში: ნ 1 და ნ 2 (ნახ. 1). დავარქვათ ეს ტერიტორია სწორინაში-

ზე O ღერძის კონტროლი ზე. ანალოგიურად, განმსაზღვრელი

y=φ 2 (x) არის სწორი უბანი მიმართულებით

ნ 2 O-ღერძი X. ფართობი სწორი მიმართულებით არის

ორივე კოორდინატთა ღერძის Nii, ჩვენ

დუბრალოდ დარეკე სწორად. Მაგალითად,

სწორი ფართობი ნაჩვენებია ნახ. 1-ში.

y=φ 1 (x) ნ 1

O a b x

დაუშვით ფუნქცია f(x, y)უწყვეტი რეგიონში დ. განიხილეთ გამოხატულება

, (24.12)

დაურეკა ორმაგი ინტეგრალიფუნქციიდან f(x, y)რეგიონის მიხედვით დ. ჯერ გამოვთვალოთ შიდა ინტეგრალი (ფრჩხილებში) ცვლადზე ზე, ითვლიან Xმუდმივი. შედეგი არის უწყვეტი ფუნქცია X:

ჩვენ ვაერთიანებთ შედეგად ფუნქციას Xდაწყებული აადრე ბ. შედეგად ვიღებთ რიცხვს

მოდით დავამტკიცოთ ორმაგი ინტეგრალის მნიშვნელოვანი თვისება.

თეორემა 1. თუ ტერიტორია დ, სწორი მიმართულებით O ზე, დაყოფილია ორ ზონად დ 1 და დ 2 სწორი ხაზი O ღერძის პარალელურად ზეან O ღერძი X, შემდეგ ორმაგი ინტეგრალი ფართობზე დტოლი იქნება იგივე ინტეგრალების ჯამის ფართობებზე დ 1 და დ 2:

მტკიცებულება.

ა) იყოს სწორი ხაზი x = გარღვევს დ on დ 1 და დ 2, სწორი მიმართულებით O ზე. მერე

ბ) დაუშვით ხაზი y = სთარღვევს დმარჯვნივ O მიმართულებით ზერეგიონი დ 1 და დ 2 (ნახ. 2). მოდით აღვნიშნოთ მ 1 (ა 1 , თ) და მ 2 (ბ 1 , თ) ხაზის გადაკვეთის წერტილები y = სთსაზღვრით ლრეგიონი დ.

წრეგიონი დ 1 შემოსაზღვრული უწყვეტი ხაზებით

y=φ 2 (x) 1) y = φ 1 (x);

დ 2 2) მრუდი ა 1 მ 1 მ 2 IN, რომლის განტოლებას ვწერთ

თ მ 1 მ 2 y = φ 1 *(x), სად φ 1 *(X) = φ 2 (X) ზე a ≤ x ≤ a 1 და

ა 1 დ 1 ბ ბ 1 ≤ x ≤ ბ, φ 1 *(X) = თზე ა 1 ≤ x ≤ ბ 1 ;

3) სწორი x = a, x = b.

რეგიონი დ 2 შემოიფარგლება ხაზებით y = φ 1 *(x),

A y= φ 2 (X),ა 1 ≤ x ≤ ბ 1 .

y=φ 1 (x) გამოვიყენოთ თეორემა შესახებ

ინტეგრაციის ინტერვალის დაყოფა:

O a ა 1 ბ 1 ბ

მიღებული ინტეგრალებიდან მეორე ჯამის სახით წარმოვადგინოთ:

+ + .

Იმიტომ რომ φ 1 *(X) = φ 2 (X) ზე a ≤ x ≤ a 1 და ბ 1 ≤ x ≤ ბ, მიღებული ინტეგრალების პირველი და მესამე იდენტურად ნულის ტოლია. აქედან გამომდინარე,

მე D = , ანუ .

ორმაგი ინტეგრალები

ლექცია 1

ორმაგი ინტეგრალები.ორმაგი ინტეგრალის განმარტება და მისი თვისებები. გამეორებული ინტეგრალები. ორმაგი ინტეგრალის შემცირება განმეორებით. ინტეგრაციის საზღვრების დაწესება. ორმაგი ინტეგრალების გამოთვლა დეკარტის კოორდინატთა სისტემაში.

ორმაგი ინტეგრალი არის განსაზღვრული ინტეგრალის ცნების განზოგადება ორი ცვლადის ფუნქციის შემთხვევისთვის. ამ შემთხვევაში, ინტეგრაციის სეგმენტის ნაცვლად, იქნება რაიმე სახის ბრტყელი ფიგურა.

დაე დარის რაღაც დახურული შეზღუდული ტერიტორია და ვ(x, y) არის ამ სფეროში განსაზღვრული და შეზღუდული თვითნებური ფუნქცია. ჩვენ ვივარაუდებთ, რომ რეგიონის საზღვრები დშედგება მრუდების სასრული რაოდენობისგან, რომლებიც მოცემულია ფორმის განტოლებებით წ=ვ(x) ან x=გ( წ), სად ვ(x) და გ(წ) არის უწყვეტი ფუნქციები.

მოდით გავყოთ ტერიტორია დშემთხვევით ჩართული ნნაწილები. მოედანი მე-ე განყოფილება აღინიშნა D სიმბოლოთი ს მე. თითოეულ განყოფილებაში ჩვენ შემთხვევით ვირჩევთ წერტილს პი,და მიეცით მას კოორდინატები ფიქსირებულ დეკარტის სისტემაში ( x i, y i). შევადგინოთ განუყოფელი ჯამიფუნქციისთვის ვ(x, y) რეგიონის მიხედვით D,ამისათვის იპოვნეთ ფუნქციის მნიშვნელობები ყველა წერტილში P iგაამრავლეთ ისინი შესაბამისი მონაკვეთების ფართობზე Ds მედა შეაჯამე ყველა მიღებული შედეგი:

დავურეკოთ დიამეტრი დიამეტრი(გ) ტერიტორიები გყველაზე დიდი მანძილი ამ ტერიტორიის სასაზღვრო წერტილებს შორის.

ორმაგი ინტეგრალი ფუნქციები ვ(x, y) დომენზე D არის ზღვარი, რომლისკენაც მიისწრაფვის ინტეგრალური ჯამების თანმიმდევრობა (1.1) დანაყოფების რაოდენობის შეუზღუდავი ზრდით n (სადაც). ეს წერია შემდეგნაირად

გაითვალისწინეთ, რომ ზოგადად რომ ვთქვათ, ინტეგრალური ჯამი მოცემული ფუნქციისა და ინტეგრაციის მოცემული დომენისთვის დამოკიდებულია დომენის დაყოფის მეთოდზე. დდა ქულების შერჩევა P i. თუმცა, თუ ორმაგი ინტეგრალი არსებობს, ეს ნიშნავს, რომ შესაბამისი ინტეგრალური ჯამების ზღვარი აღარ არის დამოკიდებული მითითებულ ფაქტორებზე. ორმაგი ინტეგრალის არსებობისთვის(ან, როგორც ამბობენ, ასე რომ ფუნქცია f(x, y) იყოს ინტეგრირებადი D დომენში), საკმარისია ინტეგრანდული ფუნქცია იყოს უწყვეტიმოცემულ ინტეგრაციის დომენში.

დაუშვით ფუნქცია ვ(x, y) ინტეგრირებადია დომენში დ. ვინაიდან ასეთი ფუნქციების შესაბამისი ინტეგრალური ჯამების ლიმიტი არ არის დამოკიდებული ინტეგრაციის დომენის დაყოფის მეთოდზე, დანაყოფი შეიძლება გაკეთდეს ვერტიკალური და ჰორიზონტალური ხაზების გამოყენებით. შემდეგ რეგიონის უმეტესი ნაწილი დექნება მართკუთხა ფორმა, რომლის ფართობი უდრის D-ს ს მე=დ x iდ y მე. აქედან გამომდინარე, ფართობის დიფერენციალი შეიძლება დაიწეროს როგორც ds=dxdy. აქედან გამომდინარე, დეკარტის კოორდინატთა სისტემაში ორმაგი ინტეგრალებიშეიძლება ჩაიწეროს ფორმაში

კომენტარი. თუ ინტეგრადი ვ(x, y)º1, მაშინ ორმაგი ინტეგრალი იქნება ინტეგრაციის რეგიონის ფართობის ტოლი:

გაითვალისწინეთ, რომ ორმაგ ინტეგრალებს აქვთ იგივე თვისებები, რაც განსაზღვრულ ინტეგრალებს. მოდით აღვნიშნოთ ზოგიერთი მათგანი.

ორმაგი ინტეგრალის თვისებები.

1 0 .ხაზოვანი თვისება. ფუნქციების ჯამის ინტეგრალი ინტეგრალების ჯამის ტოლია:

ხოლო მუდმივი ფაქტორი შეიძლება ამოღებულ იქნას ინტეგრალური ნიშნიდან:

2 0 .დანამატის თვისება. თუ ინტეგრაციის D დომენი ორ ნაწილად იყოფა, მაშინ ორმაგი ინტეგრალი ტოლი იქნება თითოეულ ამ ნაწილზე ინტეგრალების ჯამისა.:

3 0 .საშუალო მნიშვნელობის თეორემა. თუ ფუნქციავ( x, y)უწყვეტია D რეგიონში, მაშინ ამ რეგიონში არის ასეთი წერტილი(x,h) , Რა:

შემდეგი კითხვაა: როგორ გამოითვლება ორმაგი ინტეგრალები? მისი გამოთვლა შესაძლებელია დაახლოებით, ამ მიზნით შემუშავებულია ეფექტური მეთოდები შესაბამისი ინტეგრალური ჯამების შედგენისთვის, რომლებიც შემდეგ გამოითვლება რიცხობრივად კომპიუტერის გამოყენებით. ორმაგი ინტეგრალის ანალიტიკური გამოთვლისას ისინი მცირდება ორ განსაზღვრულ ინტეგრალამდე.

ორი ცვლადის ფუნქციისთვის, რომელიც მითითებულია როგორც ზ = ვ(x, წ) .

ორმაგი ინტეგრალი იწერება შემდეგნაირად:

Აქ დ– ხაზებით შემოსაზღვრული ბრტყელი ფიგურა, რომლის გამოსახულებები (ტოლობები) მოცემულია ორმაგი ინტეგრალის გამოთვლის ამოცანაში. მარცხენა და მარჯვენა არის ტოლობები, რომლებშიც არის ცვლადი მარცხნივ x, და ზემოთ და ქვემოთ – ტოლობებით, რომლებშიც არის ცვლადი მარცხნივ წ. ეს ადგილი კვლავაც არის ერთ-ერთი ყველაზე მნიშვნელოვანი ორმაგი ინტეგრალის გამოთვლის ტექნიკის გასაგებად.

გამოთვალეთ ორმაგი ინტეგრალი - ნიშნავს აღნიშნული ფიგურის ფართობის ტოლი რიცხვის პოვნას დ .

სანამ არ შევეხებით ორმაგი ინტეგრალური განმარტებები და ჩვენ ვისწავლით მის გამოთვლას. უფრო ადვილია იმის გაგება, თუ რა არის ორმაგი ინტეგრალი, როცა მის გამოსათვლელად რამდენიმე ამოცანის ამოხსნა გაქვს, ამიტომ ამ გაკვეთილის ბოლოს იპოვით ორმაგი ინტეგრალის განმარტებას. ცოტა წინ რომ გავიხედოთ, შეგვიძლია მხოლოდ აღვნიშნოთ, რომ ორმაგი ინტეგრალის განმარტება ასევე დაკავშირებულია აღნიშნულ ფიგურასთან. დ .

თუ ფიგურა დარის მართკუთხედი, მისი შემზღუდველი ყველა ხაზი სწორი ხაზებია. თუ ფიგურა დ- არის მრუდი, შემდეგ მარცხნივ და მარჯვნივ შემოიფარგლება სწორი ხაზებით, ხოლო ზემოთ და ქვემოთ მრუდი ხაზებით, მოცემული ტოლობებით, რომლებიც მოცემულია ამოცანაში. არის შემთხვევებიც, როცა ფიგურა დ- სამკუთხედი, მაგრამ უფრო ასეთ შემთხვევებზე ცოტა უფრო შორს.

ორმაგი ინტეგრალის გამოსათვლელად აუცილებელია ფიგურის მოსაზღვრე ხაზების დახარისხება დ, რომელსაც მკაცრი სახელი აქვს - ინტეგრაციის რეგიონი. დაალაგეთ მარცხნივ და მარჯვნივ და ზედა და ქვედა. ეს საჭირო იქნება როცა ორმაგი ინტეგრალის შემცირება გამეორებულ ინტეგრალზე – ორმაგი ინტეგრალის გამოთვლის მეთოდი.

მართკუთხა ფართობის შემთხვევა:

მოხრილი რეგიონის შემთხვევა:

და ეს უკვე ნაცნობი განსაზღვრული ინტეგრალების გამოსავალია, რომელშიც მოცემულია ინტეგრაციის ზედა და ქვედა საზღვრები. გამონათქვამები, რომლებიც განსაზღვრავენ ხაზებს, რომლებიც ზღუდავს ფიგურას დ, იქნება ინტეგრაციის საზღვრები ჩვეულებრივი განსაზღვრული ინტეგრალებისთვის, რომლებსაც უკვე ვუახლოვდებით.

ორმაგი ინტეგრალის შემცირება განმეორებით

მართკუთხა რეგიონის საქმე

მოდით არსებობდეს ორმაგი ინტეგრალი ასეთი ფუნქციისთვის

რომ შეაფასეთ ეს ორმაგი ინტეგრალი , უნდა დავიყვანოთ ის განმეორებით ინტეგრალამდე, რომელსაც აქვს ფორმა

ჯერ უნდა გამოთვალოთ შიდა (მარჯვნივ) განსაზღვრული ინტეგრალი, შემდეგ გარე (მარცხნივ) განსაზღვრული ინტეგრალი.

შეგიძლიათ როლების შეცვლა xდა წ

მაგალითი 1.გამოთვალეთ ორმაგი ინტეგრალი

ჩვენ ვიანგარიშებთ შიდა (მარჯვნივ) ინტეგრალს, განვიხილავთ y-ს მუდმივად. Გავიგეთ.

მაგალითი 2.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზში ჩვენ ვაშენებთ ინტეგრაციის რეგიონს:

ახლა ჩვენ გამოვთვალოთ ახლად გამოთვლილი შიდა (მარჯვნივ) გარე (მარცხნივ) ინტეგრალი:

შედეგი იქნება ამ ორმაგი ინტეგრალის გადაწყვეტა.

თავად გამოთვალეთ ორმაგი ინტეგრალი და შემდეგ გადახედეთ ამოხსნას

მოსახვევი ან სამკუთხა რეგიონის შემთხვევა

მოდით კვლავ მოგვცეს ორი ცვლადის ფუნქცია ვ(x, წ) და შეზღუდვები დ: უკვე ოდნავ განსხვავებული ტიპისაა:

ეს ჩანაწერი ნიშნავს, რომ ფიგურა დმარცხენა და მარჯვენა შეზღუდულია, როგორც სწორხაზოვანი რეგიონის შემთხვევაში - სწორი ხაზები x = ადა x = ბ, მაგრამ ქვემოთ და ზემოთ არის მრუდები, რომლებიც მოცემულია განტოლებებით და . სხვა სიტყვებით რომ ვთქვათ, და არის ფუნქციები.

დაე, ასეთ ფუნქციასაც ჰქონდეს ორმაგი ინტეგრალი

ამ ორმაგი ინტეგრალის შესაფასებლად, ჩვენ უნდა დავიყვანოთ ის განმეორებით ინტეგრალზე, რომელსაც აქვს ფორმა

აქ არის ინტეგრაციის საზღვრები ადა ბ- რიცხვები და და - ფუნქციები. სამკუთხა რეგიონის შემთხვევაში, ერთ-ერთი ფუნქცია ან არის სწორი ხაზის განტოლება. ეს შემთხვევა განხილული იქნება მაგალით 3-ში.

როგორც მართკუთხა რეგიონის შემთხვევაში, ჯერ უნდა გამოთვალოთ სწორი განსაზღვრული ინტეგრალი, შემდეგ მარცხენა განსაზღვრული ინტეგრალი.

ანალოგიურად, შეგიძლიათ როლების შეცვლა xდა წ. შემდეგ განმეორებით ინტეგრალს ექნება ფორმა

ასეთი განმეორებითი ინტეგრალი ზუსტად ასე უნდა გადაწყდეს: ჯერ - შიდა (მარჯვნივ) ინტეგრალი, შემდეგ - გარე (მარცხნივ).

მაგალითი 5.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზზე ვაშენებთ ინტეგრაციის რეგიონს და ვხედავთ, რომ ის სამკუთხაა:

ჩვენ ვიანგარიშებთ შიდა (მარჯვნივ) ინტეგრალს, განვიხილავთ x მუდმივად. Გავიგეთ.

ახლა ჩვენ გამოვთვალოთ ახლად გამოთვლილი შიდა (მარჯვნივ) გარე (მარცხნივ) ინტეგრალი. ჯერ ამ ინტეგრალს წარმოვადგენთ ინტეგრალების ჯამის სახით:

ჩვენ ვიანგარიშებთ პირველ ტერმინს:

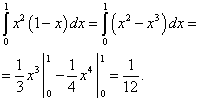
ჩვენ ვიანგარიშებთ მეორე ტერმინს:

ჩვენ ვიანგარიშებთ მესამე ტერმინს:

ჩვენ ვიღებთ ჯამს, რომელიც იქნება ამ ორმაგი ინტეგრალის ამოხსნა:

მაგალითი 6.გამოთვალეთ ორმაგი ინტეგრალი

გამოსავალი. ჩვენ ვამცირებთ ამ ორმაგ ინტეგრალს გამეორებულ ინტეგრალზე

ნახაზში ჩვენ ვაშენებთ ინტეგრაციის რეგიონს:

შედეგი იქნება ამ ორმაგი ინტეგრალის გადაწყვეტა.

x-სწორი და არასწორი წ- ინტეგრაციის სწორი და არასწორი დომენები

ეს ხდება, რომ ორმაგი ინტეგრალის ინტეგრაციის დომენი შემოიფარგლება ისეთი ხაზებით, რომ საჭირო ხდება ინტეგრაციის დომენის ნაწილებად დაყოფა და თითოეული შესაბამისი განმეორებითი ინტეგრალის ცალკე გადაჭრა. ეს ის შემთხვევებია, როდესაც:

1) ინტეგრაციის არე არის ფიგურა, რომელსაც აქვს ორი ან მეტი სწორი ან მრუდი ხაზი ქვედა ან ზედა (მარცხნივ ან მარჯვნივ) საზღვრის სახით;

2) ინტეგრაციის რეგიონი არის ფიგურა, რომლის საზღვარი ხაზები იკვეთება ორზე მეტ წერტილზე.

თუ ზემოაღნიშნული ეხება ინტეგრაციის დომენის მარცხენა ან მარჯვენა საზღვარს, ანუ ხაზებით განსაზღვრულ შეზღუდვებს, რომლებიც გამოხატულია x, მაშინ ინტეგრაციის დომენი ეწოდება x- არასწორი. თუ ხაზი წ = წ0 კვეთს შესაბამის საზღვარს მხოლოდ ერთ წერტილში და თუ საზღვარი არის მხოლოდ ერთი სწორი ხაზი ან მრუდი, მაშინ ინტეგრაციის დომენი ე.წ. x- სწორი

ანალოგიურად, თუ ხაზებით განსაზღვრული საზღვარი გამოხატული მეშვეობით წ, სწორი x = x0 იკვეთება ერთზე მეტ წერტილზე ან თუ საზღვარი არის ერთზე მეტი სწორი ხაზი ან მრუდი, მაშინ ინტეგრაციის დომენი ე.წ. წ- არასწორი. ახლა აჩვენეთ ნიშნები წ- სწორი ტერიტორია, სავარაუდოდ, საკმაოდ მარტივია.

აქამდე ჩვენ განვიხილეთ მაგალითები x-არასწორი და წ- ინტეგრაციის სწორი სფეროები. ახლა განვიხილოთ შემთხვევები, როდესაც სისწორის პირობა დარღვეულია.

მაგალითი 7.გამოთვალეთ ორმაგი ინტეგრალი, რომლის ინტეგრაციის დომენი შემოიფარგლება ხაზებით წ = x , xy = 1 , წ = 2 .

გამოსავალი. ინტეგრაციის სფეროა წ-არასწორია, რადგან მისი ქვედა საზღვარი არ შეიძლება იყოს მითითებული ერთი ხაზით წ = წ(x) . როგორც ზემოთ მოცემულ ფიგურაში ჩანს, ქვედა ზღვარი შედგება წ = x(მუქი შინდისფერი) და xy= 1 (მწვანე). ამიტომ პირდაპირი x= 1 (შავი) ჩვენ შეგვიძლია გავყოთ ინტეგრაციის დომენი ორ ნაწილად - და .

ეს ორმაგი ინტეგრალი გამოითვლება შემდეგნაირად:

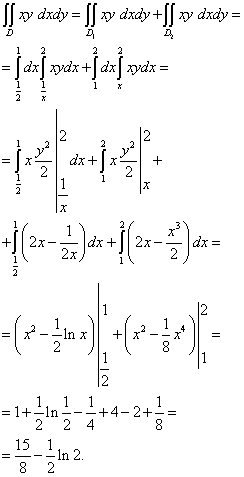
ინტეგრაციის რიგის შეცვლა

როგორც ზემოთ აღინიშნა, ორმაგი ინტეგრალის განმეორებით ინტეგრალზე შემცირების შემდეგ, შეგიძლიათ შეცვალოთ ცვლადები xდა წროლები, ან, სხვა სიტყვებით რომ ვთქვათ, შეცვალოს ინტეგრაციის რიგი.

ინტეგრაციის რიგის ცვლილება გადატანითი მნიშვნელობით შეიძლება აისახოს ო’ჰენრის შემდეგი სიტყვებით: „ასე იქცევა ჯუნგლებში მცხოვრები – ცხოველი – გალიაში მოხვედრისას და ასე იქცევა გალიაში ჩასმული ბინადარი – ადამიანი – იქცევა, როცა ეჭვების ჯუნგლებში იკარგება." ო'ჰენრის თქმით, შედეგი იგივეა და იგივე: "ჩალმერსმა წერილი დაარღვია ათას წვრილ ნაჭრად და დაიწყო მისი ძვირადღირებული ხალიჩის ტკეპნა, უკან დახევა და მასზე.” ( ო.ჰენრი. მედისონის სკვერის შეჰერეზადა.)

მაშინ, თუ ჩვენი მარცხენა ინტეგრალი ცვლადზე x, და მარჯვენა - მიერ წ, შემდეგ ინტეგრაციის რიგის შეცვლის შემდეგ ყველაფერი პირიქით იქნება. მაშინ „ახალი“ თამაშისათვის ინტეგრაციის საზღვრები უნდა იყოს „ნასესხები“ „ძველი“ X-დან, ხოლო „ახალი“ X-ის ინტეგრაციის ლიმიტები უნდა იყოს მიღებული ფორმით. შებრუნებული ფუნქცია, x-ისთვის გადაჭრით განტოლება, რომელიც ადგენს y-ს ზღვარს.

მაგალითი 8.

გამოსავალი. ინტეგრაციის რიგის შეცვლის შემდეგ, ინტეგრალი y-ზე გახდება მემარცხენე, ხოლო ინტეგრალი x-ზე - მარჯვენა. ჩვენ ვისესხებთ ინტეგრაციის საზღვრებს „ახალი“ თამაშისთვის „ძველი“ X-დან, ანუ ქვედა ზღვარი უდრის ნულს, ხოლო ზედა ზღვარი უდრის ერთს. „ძველი“ თამაშის ინტეგრაციის საზღვრები მოცემულია განტოლებებით და . x-ისთვის ამ განტოლებების ამოხსნის შემდეგ, ვიღებთ ინტეგრაციის ახალ ზღვრებს x-ისთვის:

(ქვედა) და (ზედა).

ამრიგად, ინტეგრაციის რიგის შეცვლის შემდეგ, განმეორებითი ინტეგრალი ჩაიწერება შემდეგნაირად:

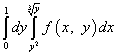ორმაგ ინტეგრალში ინტეგრაციის რიგის შეცვლის შემდეგ, ინტეგრაციის დომენი ხშირად იქცევა წ- არასწორი ან x- არასწორი (იხ. წინა პუნქტი). შემდეგ თქვენ უნდა გაყოთ ინტეგრაციის დომენი ნაწილებად და მოაგვაროთ თითოეული შესაბამისი განმეორებადი ინტეგრალი ცალ-ცალკე.

ვინაიდან ინტეგრაციის სფეროს ნაწილებად დაყოფა ბევრ სტუდენტს უქმნის გარკვეულ სირთულეებს, ჩვენ არ შემოვიფარგლებით წინა აბზაცში მოცემული მაგალითით, მაგრამ განვიხილავთ კიდევ რამდენიმე მაგალითს.

მაგალითი 9.შეცვალეთ ინტეგრაციის რიგი განმეორებადი ინტეგრალისთვის

გამოსავალი. ამრიგად, ამ განმეორებითი ინტეგრალის ინტეგრაციის არეალი შემოიფარგლება სწორი ხაზებით წ = 1 , წ = 3 , x = 0 , x = 2წ .

სხვადასხვა თანმიმდევრობით ინტეგრირებისას, რეგიონის ქვედა საზღვარი შედგება ორი სწორი ხაზისგან: ABდა ძვ.წ., რომლებიც მოცემულია განტოლებებით წ= 1 და წ = x/2, როგორც ჩანს ქვემოთ მოცემულ ფიგურაში.

ასეთი გაურკვევლობიდან გამოსავალი არის ინტეგრაციის დომენის ორ ნაწილად გაყოფა. ინტეგრაციის დომენის დაყოფა იქნება სწორი ხაზი BM. ჩვენ ვიანგარიშებთ ინტეგრაციის ახალ ზღვრებს ინვერსიული ფუნქციის მოძიებით. ამ ამოხსნის მიხედვით, განმეორებითი ინტეგრალი ინტეგრაციის რიგის შეცვლის შემდეგ იქნება ორი ინტეგრალის ჯამის ტოლი:

ბუნებრივია, იგივე იქნება ორმაგი ინტეგრალის ამოხსნა, რომელიც მცირდება ამ მაგალითის პირობებში მოცემულ განმეორებით ინტეგრალამდე.

მაგალითი 10.შეცვალეთ ინტეგრაციის რიგი განმეორებადი ინტეგრალისთვის

გამოსავალი. ასე რომ, განმეორებითი ინტეგრალის ინტეგრაციის სფერო შემოიფარგლება სწორი ხაზებით x = 0 , x= 2 და მოსახვევები და .

როგორც ქვემოთ მოცემულ ფიგურაში ჩანს, ღერძის პარალელურად სწორი ხაზი 0x, გადაკვეთს ინტეგრაციის დომენის ქვედა საზღვარს ორზე მეტ წერტილზე.

ამრიგად, ინტეგრაციის დომენს ვყოფთ სამ ნაწილად სწორი ხაზებით, რომლებიც ნახატზე შავია. ჩვენ ვიანგარიშებთ ინტეგრაციის ახალ ზღვრებს ინვერსიული ფუნქციის მოძიებით. ინტეგრაციის სამი ახალი სფეროს ლიმიტები იქნება შემდეგი.

ამ ამოხსნის მიხედვით, ინტეგრაციის რიგის შეცვლის შემდეგ განმეორებითი ინტეგრალი უდრის სამი ინტეგრალის ჯამს:

სამი ინტეგრალის იგივე ჯამი ტოლი იქნება ორმაგი ინტეგრალის, რომელიც მცირდება ამ მაგალითის პირობებში მოცემულ განმეორებით ინტეგრალამდე.

და მაინც, ფორსმაჟორული გარემოებები ხშირად ერევა სტუდენტებს უკვე წინა საფეხურზე - ინტეგრაციის საზღვრების დაწესება. შფოთვა და დაბნეულობა არ არის რაიმე საფუძვლის გარეშე: თუ ინტეგრაციის რეგიონის ნაწილებად დაყოფა, ჩვეულებრივ, საკმარისია ნახატის კარგად დათვალიერება და განმეორებითი ინტეგრალის ამოხსნა - ინტეგრალების ცხრილი, მაშინ საჭიროა გარკვეული ტრენინგის გამოცდილება საზღვრების დაყენებაში. ინტეგრაციის. მოდით გადავხედოთ მაგალითს, რომელშიც ჩვენ გავამახვილებთ ყურადღებას მხოლოდ ინტეგრაციის საზღვრების დადგენაზე და - თითქმის ავტომატურად - რეგიონის დანაწევრებაზე და გამოვტოვებთ თავად გადაწყვეტას.

მაგალითი 11.იპოვეთ ორმაგი ინტეგრალის ინტეგრაციის საზღვრები, თუ ინტეგრაციის დომენი დმოცემულია შემდეგნაირად:

წ - 2x ≤ 0;
2 წ - x ≥ 0;
xy ≤ 2.

გამოსავალი. აშკარად (მით xდა წ„მინარევების გარეშე“) ინტეგრაციის რეგიონის შემზღუდველი ხაზები არ არის მითითებული. ვინაიდან X-სთვის ისინი ყველაზე ხშირად აღმოჩნდებიან სწორი ხაზები, რომლებიც ერთ წერტილში ეხება ზედა და ქვედა საზღვრებს, გამოხატული i-ით, მაშინ ჩვენ ზუსტად ამ გზას მივყვებით. უფრო მეტიც, ინტეგრაციის რიგის შეცვლისას ვიღებთ ინტეგრაციულ რეგიონს იგივე ფართობით. მოდით მოვაგვაროთ თამაშის უთანასწორობა და მივიღოთ:

წ ≤ 2x;
წ ≥ x/2;
წ ≤ 2/x.

ჩვენ ვქმნით შედეგად ხაზებს ნახაზზე. x-ზე ინტეგრაციის საზღვრები ნამდვილად არის ხაზები x= 0 და x= 2. მაგრამ ინტეგრაციის არეალი აღმოჩნდა წ-არასწორია, რადგან მისი ზედა ზღვარი არ შეიძლება დაზუსტდეს ერთი ხაზით წ = წ(x) .

ორმაგი ინტეგრალის ძირითადი თვისებები

ორმაგი ინტეგრალის თვისებები (და მათი წარმოშობა) მსგავსია ერთი განსაზღვრული ინტეგრალის შესაბამისი თვისებების.

1°. ადიტიურობა. თუ ფუნქცია ვ(x, წ) ინტეგრირებადია დომენში დდა თუ ტერიტორია დმრუდის გამოყენებით გფართობი ნული იყოფა ორ დაკავშირებულ რეგიონად, რომლებსაც არ აქვთ საერთო შიდა წერტილები დ 1 და დ 2, შემდეგ ფუნქცია ვ(x, წ) ინტეგრირებადია თითოეულ დომენში დ 1 და დ 2 და

2°. ხაზოვანი თვისება. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, ა α და β - ნებისმიერი რეალური რიცხვი, შემდეგ ფუნქცია [ α · ვ(x, წ) + β · გ(x, წ)] ასევე ინტეგრირებადია დომენში დ, და

3°. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, მაშინ ამ ფუნქციების პროდუქტი ინტეგრირებულია დ.

4°. თუ ფუნქციები ვ(x, წ) და გ(x, წ) ორივე დომენის ინტეგრირებადია დდა ყველგან ამ მხარეში ვ(x, წ) ≤ გ(x, წ), ეს

5°. თუ ფუნქცია ვ(x, წ) ინტეგრირებადია დომენში დ, შემდეგ ფუნქცია | ვ(x, წ)| ინტეგრირებადი სფეროებში დ, და

(რა თქმა უნდა, ინტეგრაციიდან | ვ(x, წ)| ვ დინტეგრირება არ მოჰყვება ვ(x, წ) ვ დ.)

6°. საშუალო მნიშვნელობის თეორემა. თუ ორივე ფუნქციონირებს ვ(x, წ) და გ(x, წ) ინტეგრირებადია დომენებში დ, ფუნქცია გ(x, წ) არის არაუარყოფითი (არაპოზიტიური) ყველგან ამ რეგიონში, მდა მ- ფუნქციის ზუსტი ზედა და ზუსტი ქვედა საზღვრები ვ(x, წ) ტერიტორიაზე დ, მაშინ არის ნომერი μ , უთანასწორობის დაკმაყოფილება მ ≤ μ ≤ მდა ისეთი, რომ ფორმულა მოქმედებს

ორმაგი ინტეგრალის ცნებამდე მიმავალი პრობლემა.

დავუშვათ, რომ ნაწილების ფუნქცია განსაზღვრულია და ჩაწერეთ თანხა

რომელსაც ინტეგრალი ეწოდება.

პასუხი: ფუნქციისა და არჩევნის განსაზღვრული ინტეგრალის (დ.ი.) ქვეშ

Დანიშნულება:

ციფრებს უწოდებენ რიმანის ინტეგრირებადი.

თ არსებობა: იმ პირობით, რომ .

ო.ი.-ის განმარტების შესაბამისად. ჩვენ აღვნიშნავთ, რომ ინტეგრალი დამოკიდებულია ტიპზე, საზღვრებზე და, მაგრამ არ არის დამოკიდებული ცვლადის აღნიშვნის სიმბოლოზე, სხვაგვარად გამოხატული

17.1.1 და 17.1.2 პუნქტებისა და ო.ი.-ის განმარტების შესაბამისად. მოდით ჩამოვწეროთ მრუდი ტრაპეციის ფართობის ფორმულა: , ძალის მუშაობა

ზე:

ორმაგი ინტეგრალის, ინტეგრალური ჯამების ცნება.

ორმაგი ინტეგრალის არსებობა, ანუ ინტეგრალური ჯამის ზღვარი, აშკარად ჩანს, რადგან ეს ზღვარი იძლევა ცილინდრული სხეულის მოცულობას. თუმცა, ეს მსჯელობა არ არის მკაცრი. უფრო სრულყოფილ კურსებში ეს დებულება მკაცრად არის დადასტურებული და ეწოდება ორმაგი ინტეგრალის არსებობის თეორემა.

არსებობის თეორემა. ნებისმიერი ფუნქციისთვის, რომელიც უწყვეტია შეზღუდულ დახურულ რეგიონში, რომელსაც აქვს ფართობი a, არის ორმაგი ინტეგრალი, ანუ არის ინტეგრალური ჯამების ზღვარი მცირე ფართობების რაოდენობის შეუზღუდავი ზრდით, იმ პირობით, რომ თითოეული მათგანი იკუმშება წერტილი. ეს ზღვარი არ არის დამოკიდებული რეგიონის ნაწილებად დაყოფის მეთოდზე ან პუნქტების არჩევანზე

შემდგომში განვიხილავთ მხოლოდ ფუნქციებს, რომლებიც უწყვეტია ინტეგრაციის სფეროში.

არსებობის თეორემიდან გამომდინარეობს, რომ შეგვიძლია, მაგალითად, a რეგიონი დავყოთ პატარა მართკუთხედებად, სწორი გვერდებით კოორდინატთა ღერძების პარალელურად (სურ. 230). სადაც. შემდეგ თითოეულ პატარა ოთხკუთხედში წერტილის არჩევით შეგვიძლია დავწეროთ ორმაგი ინტეგრალის განმარტების მიხედვით

იმისათვის, რომ ხაზგასმით აღვნიშნოთ, რომ ორმაგი ინტეგრალი შეიძლება მივიღოთ, როგორც ფორმის ჯამის ზღვარი, აღნიშვნის ნაცვლად, ჩვენ ასევე ვიყენებთ აღნიშვნას.

გამონათქვამს ეწოდება ფართობის ელემენტი დეკარტის კოორდინატებში და უდრის მართკუთხედის ფართობს, რომლის გვერდები კოორდინატთა ღერძების პარალელურია.

გაითვალისწინეთ, რომ ინტეგრალური ჯამის შედგენისას, a ფართობის საზღვრის მიმდებარე უბნებს არ აქვთ მართკუთხედის ფორმა. თუმცა, შეიძლება დადასტურდეს, რომ ასეთი უბნების ლიმიტში მდებარე ფართობებით მართკუთხედებით ჩანაცვლების შეცდომა ნულამდე შემცირდება.

ორმაგი ინტეგრალის თვისებები

(რა თქმა უნდა, ინტეგრაციიდან | ვ(x, წ)| ვ დინტეგრირება არ მოჰყვება ვ(x, წ) ვ დ.)

კერძოდ, თუ ფუნქცია ვ(x, წ) არის უწყვეტი დდა ტერიტორია დ თანმიმდევრული, მაშინ ამ რეგიონში არის ასეთი წერტილი ( ξ , η ), Რა μ = ვ(ξ , η ) და ფორმულა (11) იღებს ფორმას