Definition av dubbelintegral. Dubbel integral

Egenskaper för dubbla integraler.

Några av egenskaperna hos dubbla integraler följer direkt av definitionen av detta begrepp och egenskaperna hos integraler, nämligen:

1. Om funktionen f(x, y) integreras i D, Den där kf(x, y)är också integrerad i denna region, och (24.4)

2. Om i området D integrerbara funktioner f(x, y) Och g(x, y), sedan funktionerna i den här domänen f(x, y) ± g(x, y) och vari

3. Om för dem som integreras i området D funktioner f(x, y) Och g(x, y) ojämlikheten håller f(x, y)≤g(x, y), Den där

(24.6)

Låt oss bevisa ytterligare några egenskaper hos dubbelintegralen:

4. Om området D uppdelad i två områden D 1 och D 2 utan gemensamma inre punkter och funktion f(x, y) kontinuerligt i regionen D, Den där

(24.7) Bevis . Helsumma över ytan D kan representeras som:

var är områdesavskiljningen D dras så att gränsen mellan D 1 och D 2 består av gränserna för skiljeväggens delar. När vi sedan passerar gränsen vid , uppnår vi jämlikhet (24.7).

5. Vid integrerbarhet på D funktioner f(x, y) i denna domän är funktionen också integrerbar | f(x, y) |, och ojämlikheten håller

(24.8)

Bevis.

varav vi, med hjälp av passagen till gränsen vid, får ojämlikhet (24.8)

6. var S D– området i regionen D. Vi erhåller beviset för detta påstående genom att ersätta integralsumman f(x, y)≡ 0.

7. Om den är integrerad i området D fungera f(x, y) tillfredsställer ojämlikheten

m ≤ f(x, y) ≤ M,

Den där (24.9)

Bevis.

Beviset genomförs genom att gå till gränsen från den uppenbara ojämlikheten

Följd.

Om vi dividerar alla delar av ojämlikhet (24.9) med D, kan vi få den så kallade medelvärdessatsen:

I synnerhet under villkoret av kontinuitet i funktionen f V D det finns en sådan punkt i den här regionen ( x 0, y 0), vart i f(x 0, y 0) = μ , det är

En annan formulering av medelvärdessatsen.

Geometrisk betydelse av dubbelintegralen.

Tänk på kroppen V, begränsad av den del av ytan som ges av ekvationen z = f(x, y), utsprång D denna yta till planet O xy och en lateral cylindrisk yta erhållen från vertikala generatriser som förbinder punkterna på ytgränsen med deras utsprång.

z=f(x,y)

y P och D Fig.2.

Vi kommer att leta efter volymen av denna kropp som gränsen för summan av volymerna av cylindrar vars baser är delar Δ S i område D, och höjder är längdsegment f(P i), där pekar P i tillhör Δ S i. När vi passerar till gränsen vid , får vi det

(24.11)

det vill säga den dubbla integralen representerar volymen av den så kallade cylinderoiden, avgränsad från ovan av ytan z = f(x, y), och under – regionen D.

Beräkning av en dubbelintegral genom att reducera den till en upprepad.

Tänk på området D, avgränsad av linjer x = a, x = b(a< b ), där φ 1 ( X) och φ 2 ( X) är kontinuerliga på [ a, b]. Sedan en rät linje parallell med koordinataxeln O på och passerar genom regionens inre punkt D, skär regiongränsen vid två punkter: N 1 och N 2 (Fig. 1). Låt oss kalla detta område korrekt i na-

på O-axelstyrning på. Likaså definierande

y=φ 2 (x) det finns ett område rätt i riktningen

N 2 O-axel X. Området i rätt riktning är

Nii av båda koordinataxlarna kommer vi

D bara kalla det rätt. Till exempel,

det korrekta området visas i fig. 1.

y=φ 1 (x) N 1

O a b x

Låt funktionen f(x, y) kontinuerligt i regionen D. Tänk på uttrycket

, (24.12)

kallad dubbel integral från funktion f(x, y) efter region D. Låt oss först beräkna den interna integralen (inom parentes) över variabeln på, räknar X permanent. Resultatet är en kontinuerlig funktion av X:

Vi integrerar den resulterande funktionen över X som sträcker sig från A innan b. Som ett resultat får vi numret

Låt oss bevisa en viktig egenskap hos dubbelintegralen.

Sats 1. Om området D, rätt i riktning O på, uppdelad i två områden D 1 och D 2 raka linjer parallella med O-axeln på eller O-axeln X, sedan den dubbla integralen över området D kommer att vara lika med summan av samma integraler över ytor D 1 och D 2:

Bevis.

a) Låt det vara en rak linje x = c raster D på D 1 och D 2, rätt i riktning O på. Sedan

b) Låt linjen y = h raster D till höger i riktning O på område D 1 och D 2 (Fig. 2). Låt oss beteckna med M 1 (a 1 , h) Och M 2 (b 1 , h) skärningspunkter för linjen y = h med en bård L område D.

y Område D 1 avgränsad av kontinuerliga linjer

y=φ 2 (x) 1) y = φ 1 (x);

D 2 2) kurva A 1 M 1 M 2 I, vars ekvation vi skriver

h M 1 M 2 y = φ 1 *(x), Var φ 1 *(X) = φ 2 (X) kl a ≤ x ≤ a 1 och

A 1 D 1 B b 1 ≤ x ≤ b, φ 1 *(X) = h på A 1 ≤ x ≤ b 1 ;

3) rakt x = a, x = b.

Område D 2 begränsat av rader y = φ 1 *(x),

A y= φ 2 (X),A 1 ≤ x ≤ b 1 .

y=φ 1 (x) Låt oss tillämpa satsen om

partitionering av integrationsintervallet:

O a a 1 b 1 b

Låt oss presentera den andra av de erhållna integralerna som en summa:

+ + .

Eftersom den φ 1 *(X) = φ 2 (X) kl a ≤ x ≤ a 1 och b 1 ≤ x ≤ b, den första och tredje av de resulterande integralerna är identiskt lika med noll. Därav,

Jag D = , det är .

DUBBEL INTEGRALER

FÖRELÄSNING 1

Dubbla integraler.Definition av dubbelintegral och dess egenskaper. Itererade integraler. Reducerar dubbla integraler till upprepade. Att sätta gränserna för integration. Beräkning av dubbla integraler i det kartesiska koordinatsystemet.

Dubbelintegralen är en generalisering av begreppet en bestämd integral till fallet med en funktion av två variabler. I det här fallet, istället för integrationssegmentet, kommer det att finnas någon form av platt figur.

Låta Där något stängt begränsat område, och f(x,y) är en godtycklig funktion definierad och begränsad i detta område. Vi kommer att anta att gränserna för regionen D består av ett ändligt antal kurvor som ges av formekvationer y=f(x) eller x=g( y), Var f(x) Och g(y) är kontinuerliga funktioner.

Låt oss dela upp området D slumpmässigt på n delar. Fyrkant i den -e sektionen kommer att betecknas med symbolen D är jag. I varje avsnitt väljer vi slumpmässigt en punkt Pi, och låt den ha koordinater i något fast kartesiskt system ( x jag, y jag). Låt oss komponera integral summa för funktion f(x,y) efter region D, för att göra detta, hitta värdena för funktionen på alla punkter P i, multiplicera dem med arean av motsvarande sektioner Ds i och summera alla erhållna resultat:

Låt oss ringa diameter diam(G) områden G det största avståndet mellan gränspunkterna för detta område.

Dubbel integral funktioner f(x,y) över domän D är gränsen till vilken sekvensen av integralsummor tenderar (1.1) med en obegränsad ökning av antalet partitioner n (vart i). Detta skrivs enligt följande

Observera att generellt sett beror integralsumman för en given funktion och en given integrationsdomän på metoden för att partitionera domänen D och välja punkter P i. Men om det finns en dubbelintegral betyder detta att gränsen för motsvarande integralsummor inte längre beror på de angivna faktorerna. För att den dubbla integralen ska existera(eller, som de säger, så att funktionen f(x,y) vara integrerbar i domän D), är det tillräckligt att integrandfunktionen är kontinuerlig i en given integrationsdomän.

Låt funktionen f(x,y) är integrerbar i domänen D. Eftersom gränsen för motsvarande integralsummor för sådana funktioner inte beror på metoden för att partitionera integrationsdomänen, kan partitionen göras med hjälp av vertikala och horisontella linjer. Sedan de flesta områden i regionen D kommer att ha en rektangulär form, vars area är lika med D är jag=D x i D y i. Därför kan areadifferentialen skrivas som ds=dxdy. Därav, i det kartesiska koordinatsystemet dubbla integraler kan skrivas i formen

Kommentar. Om integranden f(x,y)º1, då kommer dubbelintegralen att vara lika med arean för integrationsregionen:

Observera att dubbla integraler har samma egenskaper som bestämda integraler. Låt oss notera några av dem.

Egenskaper för dubbla integraler.

1 0 .Linjär egenskap. Integralen av summan av funktioner är lika med summan av integralerna:

och konstantfaktorn kan tas ur heltaltecknet:

2 0 .Additiv egenskap. Om integrationsdomänen D är uppdelad i två delar kommer dubbelintegralen att vara lika med summan av integralerna över var och en av dessa delar:

3 0 .Medelvärdessats. Om funktionen f( x,y)är kontinuerlig i region D, så finns det i denna region en sådan punkt(x,h) , Vad:

Nästa fråga är: hur beräknas dubbla integraler? Det kan beräknas ungefärligt, för detta ändamål har effektiva metoder utvecklats för att sammanställa motsvarande integralsummor, som sedan beräknas numeriskt med hjälp av en dator. Vid analytisk beräkning av dubbla integraler reduceras de till två bestämda integraler.

För en funktion av två variabler specificerade som z = f(x, y) .

Dubbelintegralen skrivs så här:

Här D– en platt figur avgränsad av linjer, vars uttryck (likheter) ges i uppgiften att beräkna dubbelintegralen. Vänster och höger är likheter där variabeln till vänster är x, och över och under – av likheter där variabeln till vänster är y. Denna plats fortsätter att vara en av de viktigaste för att förstå tekniken för att beräkna dubbelintegralen.

Beräkna dubbelintegral - betyder att hitta ett tal som är lika med arean av den nämnda figuren D .

Tills vi rör dubbla integraldefinitioner , och vi kommer att lära oss att beräkna det. Det är lättare att förstå vad en dubbelintegral är när du har löst flera problem för att beräkna den, så du hittar definitionen av en dubbelintegral i slutet av den här lektionen. Ser vi lite framåt kan vi bara notera att definitionen av en dubbelintegral också är relaterad till den nämnda figuren D .

Om figuren Där en rektangel, alla linjer som begränsar den är raka linjer. Om figuren D- är krökt, sedan till vänster och höger begränsas det av raka linjer, och över och under av krökta linjer, givet av de likheter som ges i uppgiften. Det finns också fall när en figur D- en triangel, men mer om sådana fall lite längre.

För att beräkna dubbelintegralen är det därför nödvändigt att sortera linjerna som gränsar till figuren D, som har ett strikt namn - integrationsregionen. Sortera i vänster och höger samt topp och botten. Detta kommer att krävas när reducera en dubbel integral till en itererad integral – metod för att beräkna dubbelintegralen.

Fall av ett rektangulärt område:

Fall av en krökt region:

Och detta är redan en lösning på de välbekanta bestämda integralerna, där de övre och nedre gränserna för integration är givna. Uttryck som definierar linjer som avgränsar en figur D, kommer att vara integrationens gränser för de vanliga bestämda integralerna, som vi redan närmar oss.

Att reducera en dubbelintegral till en upprepad

Fall av en rektangulär region

Låt det finnas en dubbel integral för en sådan funktion

Till utvärdera denna dubbla integral , måste vi reducera den till en itererad integral, som har formen

Först måste du beräkna den inre (höger) bestämda integralen, sedan den yttre (vänster) bestämda integralen.

Du kan byta roller x Och y

Exempel 1. Beräkna dubbelintegral

Vi beräknar den inre (höger) integralen och betraktar y som en konstant. Vi förstår.

Exempel 2. Beräkna dubbelintegral

Lösning. Vi reducerar denna dubbelintegral till en itererad integral

På ritningen konstruerar vi integrationsregionen:

Nu beräknar vi den yttre (vänster) integralen av den just beräknade inre (höger):

Resultatet blir lösningen på denna dubbla integral.

Beräkna dubbelintegralen själv och titta sedan på lösningen

Fallet med en böjd eller triangulär region

Låt oss återigen ges en funktion av två variabler f(x, y) , och begränsningarna för D: redan av en lite annan typ:

Denna post betyder att siffran D vänster och höger är begränsade, som i fallet med en rätlinjig region - raka linjer x = a Och x = b, men under och över är kurvor som ges av ekvationerna och . Med andra ord, och är funktioner.

Låt en sådan funktion också ha en dubbel integral

För att utvärdera denna dubbelintegral måste vi reducera den till en itererad integral, som har formen

Här är integrationens gränser a Och b- siffror, och och - funktioner. I fallet med en triangulär region, en av funktionerna eller är ekvationen för en rät linje. Detta fall kommer att diskuteras i exempel 3.

Som i fallet med en rätlinjig region måste du först beräkna den högra bestämda integralen, sedan den vänstra bestämda integralen.

På samma sätt kan du byta roller x Och y. Då kommer den upprepade integralen att ha formen

En sådan upprepad integral måste lösas på exakt samma sätt: först - den inre (höger) integralen, sedan - den yttre (vänster).

Exempel 5. Beräkna dubbelintegral

Lösning. Vi reducerar denna dubbelintegral till en itererad integral

På ritningen konstruerar vi integrationsregionen och ser att den är triangulär:

Vi beräknar den inre (höger) integralen och betraktar x som en konstant. Vi förstår.

Nu beräknar vi den yttre (vänster) integralen av den just beräknade inre (höger). Först presenterar vi denna integral som en summa av integraler:

Vi beräknar den första termen:

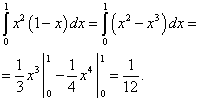
Vi beräknar den andra termen:

Vi beräknar den tredje termen:

Vi får summan, som blir lösningen på denna dubbelintegral:

Exempel 6. Beräkna dubbelintegral

Lösning. Vi reducerar denna dubbelintegral till en itererad integral

På ritningen konstruerar vi integrationsregionen:

Vi beräknar den inre (höger) integralen och betraktar x som en konstant. Vi förstår.

Nu beräknar vi den yttre (vänster) integralen av den just beräknade inre (höger):

Resultatet blir lösningen på denna dubbla integral.

x-rätt och fel y-korrekta och felaktiga integrationsdomäner

Det händer att integrationsdomänen för en dubbelintegral begränsas av sådana linjer att det blir nödvändigt att dela upp integrationsdomänen i delar och lösa varje motsvarande upprepad integral separat. Det här är fall då:

1) integrationsområdet är en figur som har två eller flera raka eller krökta linjer i form av en nedre eller övre (vänster eller höger) gräns;

2) integrationsområdet är en figur vars gräns linjerna skär varandra vid mer än två punkter.

Om ovanstående gäller den vänstra eller högra gränsen för integrationsdomänen, det vill säga de begränsningar som definieras av linjerna uttryckta i termer av x, då kallas integrationsdomänen x-fel. Om linjen y = y0 skär motsvarande gräns vid endast en punkt, och om gränsen bara är en rät linje eller kurva, kallas integrationsdomänen x-korrekt

På samma sätt, om gränsen definieras av linjer uttryckta genom y, hetero x = x0 skär i mer än en punkt eller om gränsen är mer än en rät linje eller kurva, då kallas integrationsdomänen y-fel. Visa nu skyltarna y- Det korrekta området är förmodligen ganska enkelt.

Hittills har vi tittat på exempel med x-felaktiga och y-rätta integrationsområden. Överväg nu fall när korrekthetsvillkoret överträds.

Exempel 7. Beräkna en dubbelintegral vars integrationsdomän är begränsad av linjer y = x , xy = 1 , y = 2 .

Lösning. Integrationens domän är y-felaktig, eftersom dess nedre gräns inte kan specificeras av en enda rad y = y(x) . Som framgår av figuren ovan består den nedre gränsen av y = x(mörk vinröd) och xy= 1 (grön). Därför direkt x= 1 (svart) kan vi dela upp integrationsdomänen i två delar - och .

Denna dubbelintegral beräknas enligt följande:

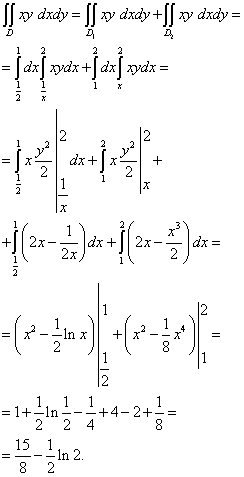
Ändra integrationsordningen

Som nämnts ovan, efter att ha reducerat dubbelintegralen till en itererad integral, kan du ändra variablerna x Och y roller, eller, med andra ord, ändra integrationsordningen.

Förändringen i integrationsordningen kan bildligt beskrivas med följande ord av O'Henry: "Så här beter sig en djungelbo - ett djur - när han kommer in i en bur, och så här är en invånare i bur - en man - beter sig när han går vilse i djungeln av tvivel." Resultatet, enligt O'Henry, är detsamma och detsamma: "Chalmers slet brevet i tusen små bitar och började slita i hans dyra matta, gå tillbaka och fram på det." ( O.Henry. Scheherazade från Madison Square.)

Sedan, om vår vänstra integral över variabeln x, och den rätta - av y, sedan efter att ha ändrat integrationsordningen kommer allt att vara tvärtom. Sedan måste integrationsgränserna för det "nya" spelet "lånas" från det "gamla" X, och integrationsgränserna för det "nya" X måste erhållas i formuläret invers funktion, lösa för x ekvationen som satte gränsen för y.

Exempel 8.

Lösning. Efter att ha ändrat integrationsordningen kommer integralen över y att bli vänsterhänt och integralen över x blir högerhänt. Vi kommer att låna integrationsgränserna för det "nya" spelet från det "gamla" X, det vill säga den nedre gränsen är lika med noll och den övre gränsen är lika med en. Gränserna för integration för det "gamla" spelet ges av ekvationerna och . Efter att ha löst dessa ekvationer för x får vi nya integrationsgränser för x:

(nedre) och (övre).

Efter att ha ändrat integrationsordningen kommer den upprepade integralen att skrivas enligt följande:

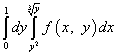Efter att ha ändrat integrationsordningen i en dubbelintegral övergår ofta integrationsdomänen till y-felaktigt eller x-felaktig (se föregående stycke). Sedan måste du dela upp integrationsdomänen i delar och lösa varje motsvarande itererade integral separat.

Eftersom att dela upp integrationsdomänen i delar innebär vissa svårigheter för många elever, kommer vi inte att begränsa oss till exemplet i föregående stycke, utan titta på ytterligare ett par exempel.

Exempel 9.Ändra integrationsordning för itererad integral

Lösning. Så, området för integration av denna itererade integral begränsas av raka linjer y = 1 , y = 3 , x = 0 , x = 2y .

När man integrerar i en annan ordning består den nedre gränsen av regionen av två raka linjer: AB Och FÖRE KRISTUS., som ges av ekvationerna y= 1 och y = x/2, som kan ses i figuren nedan.

Vägen ut ur sådan osäkerhet är att dela upp integrationsdomänen i två delar. Indelningen av integrationsdomänen kommer att vara en rak linje BM. Vi beräknar nya integrationsgränser genom att hitta den inversa funktionen. Enligt denna lösning kommer den upprepade integralen efter att ha ändrat integrationsordningen att vara lika med summan av två integraler:

Naturligtvis kommer detsamma att vara lösningen på dubbelintegralen, som reduceras till den upprepade integralen som ges i tillståndet i detta exempel.

Exempel 10.Ändra integrationsordning för itererad integral

Lösning. Så, domänen för integration av den itererade integralen är begränsad till raka linjer x = 0 , x= 2 och kurvor och .

Som kan ses i figuren nedan, en rät linje parallell med axeln 0x, kommer att skära den nedre gränsen för integrationsdomänen vid mer än två punkter.

Därför delar vi in integrationsdomänen i tre delar med raka linjer, som är ritade i svart i figuren. Vi beräknar nya integrationsgränser genom att hitta den inversa funktionen. Gränserna för de tre nya integrationsområdena blir följande.

Enligt denna lösning kommer den upprepade integralen efter att ha ändrat integrationsordningen att vara lika med summan av tre integraler:

Samma summa av tre integraler kommer att vara lika med dubbelintegralen, vilket reduceras till den upprepade integralen som ges i villkoret i detta exempel.

Och ändå stör force majeure-förhållanden ofta eleverna redan i det föregående steget - sätter gränserna för integrationen. Ångest och förvirring är inte utan någon grund: om för att dela upp integrationsregionen i delar räcker det vanligtvis att titta noga på ritningen och att lösa den upprepade integralen - tabellen över integraler, då behövs viss träningserfarenhet för att sätta gränserna integration. Låt oss gå igenom ett exempel där vi bara kommer att fokusera på att sätta gränserna för integration och - nästan automatiskt - på att dela upp regionen och utelämna själva lösningen.

Exempel 11. Hitta gränserna för integration av en dubbel integral om domänen för integration D ges enligt följande:

y - 2x ≤ 0;
2 år - x ≥ 0;
xy ≤ 2.

Lösning. Explicit (via x Och y"utan föroreningar") linjerna som begränsar integrationsregionen specificeras inte. Eftersom de för X oftast visar sig vara raka linjer som vid en punkt vidrör de övre och nedre gränserna, uttryckta genom i:et, kommer vi att gå exakt längs denna väg. Vid ändring av integrationsordningen får vi dessutom en integrationsregion med samma område. Låt oss lösa ojämlikheterna för spelet och få:

y ≤ 2x;
y ≥ x/2;
y ≤ 2/x.

Vi bygger de resulterande linjerna på ritningen. Gränserna för integration över x är verkligen linjerna x= 0 och x= 2 . Men området för integration visade sig vara y-felaktig, eftersom dess övre gräns inte kan specificeras med en enda rad y = y(x) .

Dubbelintegralens grundläggande egenskaper

Egenskaperna för en dubbelintegral (och deras härledning) liknar motsvarande egenskaper hos en enda bestämd integral.

1°. Additivitet. Om funktionen f(x, y) är integrerbar i domänen D och om området D med hjälp av en kurva G area noll är uppdelad i två sammankopplade regioner som inte har några gemensamma inre punkter D 1 och D 2, sedan funktionen f(x, y) är integrerbar i var och en av domänerna D 1 och D 2, och

2°. Linjär egenskap. Om funktionerna f(x, y) Och g(x, y) är integrerbara i domäner D, A α Och β - alla reella tal, sedan funktionen [ α · f(x, y) + β · g(x, y)] är också integrerbar i domänen D, och

3°. Om funktionerna f(x, y) Och g(x, y) är integrerbara i domäner D, då kan produkten av dessa funktioner integreras i D.

4°. Om funktionerna f(x, y) Och g(x, y) båda är domänintegrerbara D och överallt i detta område f(x, y) ≤ g(x, y), Den där

5°. Om funktionen f(x, y) är integrerbar i domänen D, sedan funktionen | f(x, y)| integreras i områden D, och

(Naturligtvis från integrerbarhet | f(x, y)| V D integrerbarhet följer inte f(x, y) V D.)

6°. Medelvärdessats. Om båda fungerar f(x, y) Och g(x, y) är integrerbara i domäner D, funktion g(x, y) är icke-negativ (icke-positiv) överallt i denna region, M Och m- Exakta övre och exakta nedre gränser för funktionen f(x, y) i området D, så finns det ett nummer μ , som tillfredsställer ojämlikheten m ≤ μ ≤ M och så att formeln är giltig

Ett problem som leder till begreppet dubbelintegral.

Låt oss anta att delarnas funktion är definierad och skriv ner beloppet

som kallas integral.

S: Under den bestämda integralen (d.i.) av funktionen och valet

Beteckning:

Siffrorna kallas Riemann integrable on .

T. existens: Förutsatt att .

I enlighet med definitionen av o.i. vi noterar att integralen beror på typen, gränserna och, men beror inte på symbolen för variabelbeteckningen, annars uttryckt

I enlighet med punkterna 17.1.1 och 17.1.2 och definitionen av o.i. Låt oss skriva ner formeln för arean av en kurvlinjär trapets: , kraftarbete

på:

Begreppet dubbel integral, integral summor.

Förekomsten av en dubbel integral, d.v.s. en gräns för integralsumman för, verkar uppenbar, eftersom denna gräns ger volymen av en cylindrisk kropp. Detta resonemang är dock inte rigoröst. I mer kompletta kurser är detta påstående strikt bevisat och kallas satsen om förekomsten av en dubbelintegral.

Existenssats. För varje funktion som är kontinuerlig i ett avgränsat slutet område med area a, finns det en dubbel integral, det vill säga det finns en gräns för integralsummor med en obegränsad ökning av antalet små områden, förutsatt att var och en av dem drar ihop sig till en punkt. Denna gräns beror inte på metoden för att dela upp regionen i delar eller på valet av punkter

I det följande kommer vi endast att betrakta funktioner som är kontinuerliga inom området integration.

Av existenssatsen följer att vi till exempel kan dela upp området a i små rektanglar med raka sidor parallella med koordinataxlarna (bild 230). Vart i. Genom att sedan välja en punkt i varje liten rektangel kan vi skriva, enligt definitionen av dubbelintegralen

För att understryka att dubbelintegralen kan erhållas som gränsen för en summa av formen, istället för notationen, använder vi också notationen

Uttrycket kallas areaelement i kartesiska koordinater och är lika med arean av en rektangel med sidor parallella med koordinataxlarna.

Observera att när man sammanställer integralsumman har områdena intill gränsen för området a inte formen av rektanglar. Det kan dock bevisas att felet från att ersätta sådana områden med rektanglar med områden i gränsen kommer att reduceras till noll.

Egenskaper för dubbla integraler

Egenskaperna för en dubbelintegral (och deras härledning) liknar motsvarande egenskaper hos en enda bestämd integral.

3°. Om funktionerna f(x, y) Och g(x, y) är integrerbara i domäner D, då kan produkten av dessa funktioner integreras i D.

4°. Om funktionerna f(x, y) Och g(x, y) båda är domänintegrerbara D och överallt i detta område f(x, y) ≤ g(x, y), Den där

5°. Om funktionen f(x, y) är integrerbar i domänen D, sedan funktionen | f(x, y)| integreras i områden D, och

(Naturligtvis från integrerbarhet | f(x, y)| V D integrerbarhet följer inte f(x, y) V D.)

I synnerhet om funktionen f(x, y) är kontinuerlig i D, och området D sammanhängande, då i den här regionen finns det en sådan punkt ( ξ , η ), Vad μ = f(ξ , η ), och formel (11) tar formen