ვექტორთა ნამრავლი. ვექტორების შერეული პროდუქტი

განმარტება. ვექტორის ნამრავლი a (გამრავლება) ვექტორით (გამრავლებით), რომელიც არ არის მასთან კოლინარული, არის მესამე ვექტორი c (პროდუქტი), რომელიც აგებულია შემდეგნაირად:

1) მისი მოდული რიცხობრივად ტოლია პარალელოგრამის ფართობის ნახ. 155), აგებულია ვექტორებზე, ანუ ტოლია აღნიშნული პარალელოგრამის სიბრტყის პერპენდიკულარული მიმართულების;

3) ამ შემთხვევაში c ვექტორის მიმართულება არჩეულია (ორი შესაძლოდან) ისე, რომ c ვექტორებმა შექმნან მარჯვენა სისტემა (§ 110).

აღნიშვნა: ან

განმარტების დამატება. თუ ვექტორები ხაზოვანია, მაშინ ფიგურის (პირობითად) პარალელოგრამის გათვალისწინებით, ბუნებრივია ნულოვანი ფართობის მინიჭება. მაშასადამე, კოლინარული ვექტორების ვექტორული ნამრავლი ითვლება ნულოვანი ვექტორის ტოლად.

ვინაიდან ნულ ვექტორს შეიძლება მიენიჭოს ნებისმიერი მიმართულება, ეს კონვენცია არ ეწინააღმდეგება განმარტების მე-2 და მე-3 პუნქტებს.

შენიშვნა 1. ტერმინში „ვექტორული ნამრავლი“ პირველი სიტყვა მიუთითებს იმაზე, რომ მოქმედების შედეგი არის ვექტორი (სკალარული ნამრავლისგან განსხვავებით; შდრ. § 104, შენიშვნა 1).

მაგალითი 1. იპოვეთ ვექტორული ნამრავლი, სადაც არის სწორი კოორდინატთა სისტემის ძირითადი ვექტორები (სურ. 156).

1. ვინაიდან ძირითადი ვექტორების სიგრძეები მასშტაბის ერთეულის ტოლია, პარალელოგრამის (კვადრატის) ფართობი რიცხობრივად ერთის ტოლია. მაშასადამე, ვექტორული ნამრავლის მოდული უდრის ერთს.

2. ვინაიდან სიბრტყეზე პერპენდიკულარული არის ღერძი, სასურველი ვექტორული ნამრავლი არის ვექტორი k ვექტორის თანამიმართული; და რადგან ორივე მათგანს აქვს მოდული 1, საჭირო ჯვარედინი პროდუქტი არის k ან -k.

3. ამ ორი შესაძლო ვექტორიდან პირველი უნდა ავირჩიოთ, ვინაიდან k ვექტორები ქმნიან მარჯვენა სისტემას (ხოლო ვექტორები ქმნიან მარცხენას).

მაგალითი 2. იპოვეთ ჯვარედინი ნამრავლი

გამოსავალი. როგორც მაგალითად 1-ში, ჩვენ დავასკვნათ, რომ ვექტორი არის k ან -k. მაგრამ ახლა ჩვენ უნდა ავირჩიოთ -k, რადგან ვექტორები ქმნიან სწორ სისტემას (და ვექტორები ქმნიან მარცხენას). Ისე,

მაგალითი 3 ვექტორებს აქვთ სიგრძე 80 და 50 სმ შესაბამისად და ქმნიან 30° კუთხეს. მეტრის სიგრძის ერთეულის სახით იპოვეთ ვექტორული ნამრავლის სიგრძე a

გამოსავალი. ვექტორებზე აგებული პარალელოგრამის ფართობი ტოლია სასურველი ვექტორული ნამრავლის სიგრძე უდრის

მაგალითი 4. იპოვეთ იგივე ვექტორების ჯვარედინი ნამრავლის სიგრძე, აიღეთ სანტიმეტრი სიგრძის ერთეულით.

გამოსავალი. ვინაიდან ვექტორებზე აგებული პარალელოგრამის ფართობი უდრის ვექტორული ნამრავლის სიგრძეს, არის 2000 სმ, ე.ი.

მე-3 და მე-4 მაგალითების შედარება აჩვენებს, რომ ვექტორის სიგრძე დამოკიდებულია არა მხოლოდ ფაქტორების სიგრძეზე, არამედ სიგრძის ერთეულის არჩევანზე.

ვექტორული პროდუქტის ფიზიკური მნიშვნელობა.ვექტორული ნამრავლით წარმოდგენილი მრავალი ფიზიკური სიდიდედან განვიხილავთ მხოლოდ ძალის მომენტს.

ვთქვათ A არის ძალის გამოყენების წერტილი. O წერტილთან მიმართებით ძალის მომენტს ეწოდება ვექტორული ნამრავლი. ვინაიდან ამ ვექტორული ნამრავლის მოდული რიცხობრივად უდრის პარალელოგრამის ფართობს (ნახ. 157), მომენტის მოდული უდრის ფუძის ნამრავლს სიმაღლით, ანუ ძალა გამრავლებული მანძილით O წერტილიდან სწორ ხაზამდე, რომლის გასწვრივაც მოქმედებს ძალა.

მექანიკაში დადასტურებულია, რომ ხისტი სხეულის წონასწორობისთვის აუცილებელია, რომ არა მხოლოდ სხეულზე მიმართული ძალების გამომსახველი ვექტორების ჯამი, არამედ ძალების მომენტების ჯამიც იყოს ნულის ტოლი. იმ შემთხვევაში, როდესაც ყველა ძალა პარალელურია ერთი და იმავე სიბრტყის პარალელურად, მომენტების გამოსახული ვექტორების დამატება შეიძლება შეიცვალოს მათი მოდულების შეკრებითა და გამოკლებით. მაგრამ ძალების თვითნებური მიმართულებისთვის, ასეთი ჩანაცვლება შეუძლებელია. ამის შესაბამისად, ჯვარედინი პროდუქტი განისაზღვრება ზუსტად როგორც ვექტორი და არა როგორც რიცხვი.

სამი ვექტორის შერეული პროდუქტი და მისი თვისებები

შერეული პროდუქტისამ ვექტორს ეწოდება რიცხვი ტოლი . აღინიშნება . აქ პირველი ორი ვექტორი მრავლდება ვექტორულად და შემდეგ მიღებული ვექტორი მრავლდება სკალარულად მესამე ვექტორზე. ცხადია, ასეთი პროდუქტი რაღაც რიცხვია.

განვიხილოთ შერეული პროდუქტის თვისებები.

1. გეომეტრიული გრძნობაშერეული პროდუქტი. შერეული პროდუქტი 3 ვექტორი, ნიშანმდე, უდრის ამ ვექტორებზე აგებული პარალელეპიპედის მოცულობას, როგორც კიდეებზე, ე.ი. .

   ამრიგად, და .

   

   მტკიცებულება. გადავდოთ ვექტორები საერთო საწყისიდან და ავაშენოთ მათზე პარალელეპიპედი. მოდით აღვნიშნოთ და აღვნიშნოთ, რომ. Განმარტებით წერტილოვანი პროდუქტი

   ვივარაუდოთ, რომ და აღნიშნავს მეშვეობით თპარალელეპიპედის სიმაღლეს ვპოულობთ .

   ამრიგად, ზე

   თუ , მაშინ და . შესაბამისად,.

   ამ ორივე შემთხვევის შერწყმით მივიღებთ ან .

   ამ თვისების მტკიცებულებიდან, კერძოდ, გამომდინარეობს, რომ თუ ვექტორთა სამმაგი სწორია, მაშინ შერეული ნამრავლი და თუ დარჩა, მაშინ .

2. ნებისმიერი ვექტორისთვის , ტოლობა

   ამ თვისების დადასტურება გამომდინარეობს თვისებიდან 1. მართლაც, ადვილია იმის ჩვენება, რომ და . უფრო მეტიც, ნიშნები "+" და "-" აღებულია ერთდროულად, რადგან კუთხეები ვექტორებს შორის და და არის ორივე მწვავე ან ბლაგვი.

3. როდესაც ნებისმიერი ორი ფაქტორი იცვლება, შერეული პროდუქტი ცვლის ნიშანს.

   მართლაც, თუ გავითვალისწინებთ შერეულ პროდუქტს, მაშინ, მაგალითად, ან

4. შერეული პროდუქტი, თუ და მხოლოდ მაშინ, თუ ერთ-ერთი ფაქტორი ნულის ტოლია ან ვექტორები თანაპლანსურია.

   მტკიცებულება.

   ამრიგად, 3 ვექტორის თანაბარობის აუცილებელი და საკმარისი პირობაა მათი შერეული ნამრავლის ნულის ტოლობა. გარდა ამისა, აქედან გამომდინარეობს, რომ სამი ვექტორი ქმნის საფუძველს სივრცეში, თუ .

   თუ ვექტორები მოცემულია კოორდინატთა სახით, მაშინ შეიძლება აჩვენოს, რომ მათი შერეული პროდუქტი ნაპოვნია ფორმულით:

   .

   ამრიგად, შერეული პროდუქტი უდრის მესამე რიგის განმსაზღვრელს, რომლის პირველი ხაზი შეიცავს პირველი ვექტორის კოორდინატებს, მეორე ხაზი შეიცავს მეორე ვექტორის კოორდინატებს, ხოლო მესამე ხაზი შეიცავს მესამე ვექტორის კოორდინატებს.

   მაგალითები.

ანალიტიკური გეომეტრია სივრცეში

განტოლება F(x, y, z)= 0 განსაზღვრავს სივრცეში ოქსიზირაღაც ზედაპირი, ე.ი. წერტილების ლოკუსი, რომლის კოორდინატები x, y, zდააკმაყოფილეთ ეს განტოლება. ამ განტოლებას ეწოდება ზედაპირის განტოლება და x, y, z- მიმდინარე კოორდინატები.

თუმცა, ხშირად ზედაპირი არ არის განსაზღვრული განტოლებით, არამედ, როგორც სივრცეში წერტილების ერთობლიობა, რომლებსაც აქვთ ამა თუ იმ თვისება. ამ შემთხვევაში საჭიროა ზედაპირის განტოლების პოვნა, მისი გეომეტრიული თვისებებიდან გამომდინარე.

თვითმფრინავი.

ნორმალური სიბრტყის ვექტორი.

მოცემულ წერტილში გამავალი თვითმფრინავის განტოლება

განვიხილოთ თვითნებური სიბრტყე σ სივრცეში. მისი პოზიცია განისაზღვრება ამ სიბრტყეზე პერპენდიკულარული ვექტორის და გარკვეული ფიქსირებული წერტილის დაყენებით M0(x0, y 0, z0) წევს თვითმფრინავში σ.

σ სიბრტყის პერპენდიკულარულ ვექტორს ეწოდება ნორმალურიამ სიბრტყის ვექტორი. დაე, ვექტორს ჰქონდეს კოორდინატები.

გამოვყავით მოცემულ წერტილში გამავალი σ სიბრტყის განტოლება M0და აქვს ნორმალური ვექტორი. ამისათვის აიღეთ თვითნებური წერტილი σ სიბრტყეზე M(x, y, z)და განიხილეთ ვექტორი.

ნებისმიერი წერტილისთვის მÎ σ ვექტორი.მაშასადამე, მათი სკალარული ნამრავლი ნულის ტოლია. ეს თანასწორობა არის ის პირობა, რომ წერტილი მО ს. იგი მოქმედებს ამ სიბრტყის ყველა პუნქტზე და ირღვევა წერტილისთანავე მსიბრტყის გარეთ იქნება σ.

თუ რადიუსის ვექტორით აღვნიშნავთ წერტილებს მ, არის წერტილის რადიუსის ვექტორი M0, მაშინ განტოლება შეიძლება დაიწეროს როგორც

ეს განტოლება ე.წ ვექტორისიბრტყის განტოლება. ჩავწეროთ კოორდინატულად. Მას შემდეგ

ამრიგად, ჩვენ მივიღეთ მოცემულ წერტილში გამავალი სიბრტყის განტოლება. ამრიგად, სიბრტყის განტოლების შედგენის მიზნით, თქვენ უნდა იცოდეთ ნორმალური ვექტორის კოორდინატები და სიბრტყეზე მდებარე რომელიმე წერტილის კოორდინატები.

გაითვალისწინეთ, რომ სიბრტყის განტოლება არის 1-ლი ხარისხის განტოლება მიმდინარე კოორდინატებთან მიმართებაში. x, yდა ზ.

მაგალითები.

სიბრტყის ზოგადი განტოლება

შეიძლება აჩვენოს, რომ პირველი ხარისხის ნებისმიერი განტოლება დეკარტის კოორდინატებთან მიმართებაში x, y, zარის რაღაც სიბრტყის განტოლება. ეს განტოლება იწერება როგორც:

Axe+By+Cz+D=0

და დაურეკა ზოგადი განტოლებათვითმფრინავი და კოორდინატები A, B, Cაქ არის სიბრტყის ნორმალური ვექტორის კოორდინატები.

განვიხილოთ ზოგადი განტოლების კონკრეტული შემთხვევები. მოდით გავარკვიოთ, როგორ მდებარეობს სიბრტყე კოორდინატთა სისტემის მიმართ, თუ განტოლების ერთი ან მეტი კოეფიციენტი ქრება.

A არის ღერძზე სიბრტყით მოწყვეტილი სეგმენტის სიგრძე ოქსი. ანალოგიურად, შეიძლება ამის ჩვენება ბდა გარის ღერძებზე განხილული სიბრტყით მოწყვეტილი მონაკვეთების სიგრძეები ოიდა ოზი.

სიბრტყის ასაგებად მოსახერხებელია სიბრტყის განტოლების გამოყენება სეგმენტებში.

ეს ონლაინ კალკულატორი ითვლის ვექტორების ჯვარედინი ნამრავლს. მოცემულია დეტალური გადაწყვეტა. ვექტორების ჯვარედინი ნამრავლის გამოსათვლელად შეიყვანეთ ვექტორების კოორდინატები უჯრედებში და დააწკაპუნეთ ღილაკზე "გამოთვლა".

×

გაფრთხილება

გაასუფთავო ყველა უჯრედი?

დახურეთ გასუფთავება

მონაცემთა შეყვანის ინსტრუქცია.რიცხვები შეყვანილია როგორც მთელი რიცხვები (მაგალითები: 487, 5, -7623 და ა.შ.), ათობითი რიცხვები (მაგ. 67., 102.54 და ა.შ.) ან წილადები. წილადი უნდა იყოს აკრეფილი a/b ფორმით, სადაც a და b (b>0) არის მთელი ან ათობითი რიცხვები. მაგალითები 45/5, 6.6/76.4, -7/6.7 და ა.შ.

ვექტორების ჯვარედინი ნამრავლი

სანამ გადავიდეთ ვექტორების ვექტორული ნამრავლის განსაზღვრაზე, განიხილეთ ცნებები შეკვეთილი ვექტორების სამმაგი, ვექტორების მარცხენა სამმაგი, ვექტორების მარჯვენა სამმაგი.

განმარტება 1. სამი ვექტორი ეწოდება შეუკვეთა სამმაგი(ან სამმაგი) თუ მითითებულია ამ ვექტორებიდან რომელია პირველი, რომელი მეორე და რომელი მესამე.

ჩაწერა cba- ნიშნავს - პირველი არის ვექტორი გ, მეორე არის ვექტორი ბდა მესამე არის ვექტორი ა.

განმარტება 2. არაერთობლივი ვექტორების სამმაგი abcეწოდება მარჯვენა (მარცხნივ), თუ საერთო საწყისამდე დაყვანისას ეს ვექტორები განლაგებულია ისე, როგორც განლაგებულია მარჯვენა (მარცხენა) ხელის დიდი, მოუხვევი საჩვენებელი და შუა თითები.

განმარტება 2 შეიძლება სხვაგვარად ჩამოყალიბდეს.

განმარტება 2. არაერთობლივი ვექტორების სამმაგი abcეწოდება მარჯვენა (მარცხნივ), თუ საერთო საწყისამდე დაყვანისას ვექტორი გმდებარეობს ვექტორებით განსაზღვრული სიბრტყის მეორე მხარეს ადა ბ, საიდანაც უმოკლესი შემობრუნება არომ ბშესრულებული საათის ისრის საწინააღმდეგოდ (საათის ისრის მიმართულებით).

ვექტორული ტრიო abcნაჩვენებია ნახ. 1 არის სწორი და სამმაგი abcნაჩვენებია ნახ. დარჩა 2.

თუ ვექტორების ორი სამეული მარჯვნივ ან მარცხნივ არის, მაშინ ამბობენ, რომ მათ აქვთ იგივე ორიენტაცია. წინააღმდეგ შემთხვევაში, ამბობენ, რომ ისინი საპირისპირო ორიენტაციის არიან.

განმარტება 3. კარტეზიულ ან აფინურ კოორდინატულ სისტემას ეწოდება მარჯვენა (მარცხნივ), თუ სამი ძირითადი ვექტორი ქმნის მარჯვენა (მარცხნივ) სამეულს.

დაზუსტებისთვის, შემდეგში განვიხილავთ მხოლოდ მარჯვენა კოორდინატულ სისტემებს.

განმარტება 4. ვექტორული ხელოვნებავექტორი ავექტორზე ბვექტორი ეწოდება თან, აღინიშნება სიმბოლოთი c=[აბ] (ან c=[ა, ბ], ან c=a×b) და აკმაყოფილებს შემდეგ სამ მოთხოვნას:

• ვექტორის სიგრძე თანუდრის ვექტორების სიგრძის ნამრავლს ადა ბკუთხის სინუსამდე φ მათ შორის:

|გ|=|[აბ]|=|ა||ბ|sinφ;

(1)

• ვექტორი თანორთოგონალური თითოეული ვექტორის მიმართ ადა ბ;
• ვექტორი გმიმართულია ისე, რომ სამი abcმართალია.

ვექტორების ჯვარედინი ნამრავლს აქვს შემდეგი თვისებები:

• [აბ]=−[ბა] (ანტიპერმუტაციულობაფაქტორები);
• [(λa)ბ]=λ [აბ] (თავსებადობარიცხვით ფაქტორთან შედარებით);
• [(ა+ბ)გ]=[აგ]+[ბგ] (განაწილებავექტორთა ჯამთან შედარებით);
• [აა]=0 ნებისმიერი ვექტორისთვის ა.

ვექტორთა ჯვარედინი ნამრავლის გეომეტრიული თვისებები

თეორემა 1. იმისათვის, რომ ორი ვექტორი იყოს კოლინარული, აუცილებელია და საკმარისია, რომ მათი ვექტორული ნამრავლი იყოს ნულის ტოლი.

მტკიცებულება. საჭიროება. მოდით ვექტორები ადა ბკოლინარული. მაშინ მათ შორის კუთხე არის 0 ან 180° და sinφ=sin180=ცოდვა 0=0. ამიტომ, გამოხატვის (1) გათვალისწინებით, ვექტორის სიგრძე გუდრის ნულს. მერე გნულოვანი ვექტორი.

ადეკვატურობა. მოდით ვექტორების ჯვარედინი ნამრავლი ადა ბგადაიყვანეთ ნულამდე: [ აბ]=0. დავამტკიცოთ, რომ ვექტორები ადა ბკოლინარული. თუ რომელიმე ვექტორიდან მაინც ადა ბნულოვანი, მაშინ ეს ვექტორები კოლინარულია (რადგან ნულოვან ვექტორს აქვს განუსაზღვრელი მიმართულება და შეიძლება ჩაითვალოს ნებისმიერი ვექტორის კოლინარად).

თუ ორივე ვექტორი ადა ბნულოვანი, მაშინ | ა|>0, |ბ|>0. შემდეგ [ აბ]=0 და (1)-დან გამომდინარეობს, რომ sinφ=0. აქედან გამომდინარე ვექტორები ადა ბკოლინარული.

თეორემა დადასტურდა.

თეორემა 2. ვექტორული ნამრავლის სიგრძე (მოდული) [ აბ] უდრის ფართობს სვექტორებზე აგებული პარალელოგრამი საერთო საწყისამდე ადა ბ.

მტკიცებულება. მოგეხსენებათ, პარალელოგრამის ფართობი უდრის ამ პარალელოგრამის მიმდებარე გვერდების ნამრავლს და მათ შორის კუთხის სინუსს. შესაბამისად:

მაშინ ამ ვექტორების ჯვარედინი ნამრავლს აქვს ფორმა:

განმსაზღვრელი პირველი რიგის ელემენტებზე გავაფართოვოთ, მივიღებთ ვექტორის დაშლას a×bსაფუძველი მე, ჯ, კ, რომელიც უდრის ფორმულას (3).

თეორემა 3-ის დადასტურება. შეადგინეთ საფუძვლების ვექტორების ყველა შესაძლო წყვილი მე, ჯ, კდა გამოთვალეთ მათი ვექტორული ნამრავლი. გასათვალისწინებელია, რომ საბაზისო ვექტორები ორთოგონალურია, ქმნიან მარჯვენა სამეულს და აქვთ ერთეული სიგრძე (სხვა სიტყვებით რომ ვთქვათ, შეგვიძლია ვივარაუდოთ, რომ მე={1, 0, 0}, ჯ={0, 1, 0}, კ=(0, 0, 1)). მაშინ გვაქვს:

ბოლო თანასწორობიდან და მიმართებებიდან (4) ვიღებთ:

შეადგინეთ 3×3 მატრიცა, რომლის პირველი რიგი არის საბაზისო ვექტორები მე, ჯ, კ,ხოლო დარჩენილი რიგები ივსება ვექტორების ელემენტებით ადა ბ.

სანამ ვექტორული ნამრავლის ცნებას მოვიყვანთ, მივმართოთ a → , b → , c → ვექტორების მოწესრიგებული სამეულის ორიენტაციის საკითხს სამგანზომილებიან სივრცეში.

დასაწყისისთვის, ერთი წერტილიდან გამოვყოთ a → , b → , c → ვექტორები. a → , b → , c → სამმაგი ორიენტაცია არის მარჯვნივ ან მარცხნივ, რაც დამოკიდებულია c → ვექტორის მიმართულებაზე. იმ მიმართულებიდან, რომლითაც კეთდება უმოკლესი ბრუნი a → b → ვექტორიდან c → → ვექტორის ბოლოდან, განისაზღვროს სამმაგი a → , b → , c →.

თუ უმოკლეს ბრუნვა არის საათის ისრის საწინააღმდეგოდ, მაშინ ვექტორების სამმაგი a → , b → , c → ე.წ. უფლებათუ საათის ისრის მიმართულებით - დატოვა.

შემდეგი, აიღეთ ორი არასწორხაზოვანი ვექტორი a → და b → . შემდეგ გადავდოთ ვექტორები A B → = a → და A C → = b → A წერტილიდან. ავაშენოთ ვექტორი A D → = c →, რომელიც ერთდროულად არის პერპენდიკულარული A B → და A C →. ამრიგად, A D → = c → ვექტორის აგებისას, ჩვენ შეგვიძლია გავაკეთოთ ორი რამ, მივცეთ მას ერთი მიმართულება ან საპირისპირო (იხ. ილუსტრაცია).

a → , b → , c → ვექტორების მოწესრიგებული სამეული შეიძლება იყოს, როგორც გავარკვიეთ, მარჯვნივ ან მარცხნივ, ვექტორის მიმართულებიდან გამომდინარე.

ზემოაღნიშნულიდან შეგვიძლია შემოვიტანოთ ვექტორული პროდუქტის განმარტება. ეს განმარტება მოცემულია ორ ვექტორზე, რომლებიც განსაზღვრულია სამგანზომილებიანი სივრცის მართკუთხა კოორდინატულ სისტემაში.

განმარტება 1

ორი ვექტორის a → და b → ვექტორული ნამრავლი ჩვენ დავარქმევთ ისეთ ვექტორს, რომელიც მოცემულია სამგანზომილებიანი სივრცის მართკუთხა კოორდინატულ სისტემაში, რომ:

• თუ a → და b → ვექტორები წრფივია, ის იქნება ნული;
• ის იქნება პერპენდიკულარული როგორც a →​​ ვექტორის, ასევე b ვექტორის მიმართ, ე.ი. ∠ a → c → = ∠ b → c → = π 2;
• მისი სიგრძე განისაზღვრება ფორმულით: c → = a → b → sin ∠ a → , b → ;
• a → , b → , c → ვექტორების სამეულს იგივე ორიენტაცია აქვს, რაც მოცემულ კოორდინატულ სისტემას.

a → და b → ვექტორების ჯვარედინი ნამრავლს აქვს შემდეგი აღნიშვნა: a → × b → .

ჯვარედინი პროდუქტის კოორდინატები

ვინაიდან ნებისმიერ ვექტორს აქვს გარკვეული კოორდინატები კოორდინატთა სისტემაში, შესაძლებელია შემოვიტანოთ ვექტორული ნამრავლის მეორე განმარტება, რომელიც საშუალებას მოგცემთ იპოვოთ მისი კოორდინატები ვექტორების მოცემული კოორდინატებიდან.

განმარტება 2

სამგანზომილებიანი სივრცის მართკუთხა კოორდინატულ სისტემაში ორი ვექტორის ვექტორული ნამრავლი a → = (a x ; a y ; a z) და b → = (b x ; b y ; b z) მოვუწოდებთ ვექტორს c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , სადაც i → , j → , k → არის კოორდინატული ვექტორები.

ვექტორული ნამრავლი შეიძლება წარმოდგენილი იყოს, როგორც მესამე რიგის კვადრატული მატრიცის განმსაზღვრელი, სადაც პირველი მწკრივი არის ორტა ვექტორები i → , j → , k → , მეორე რიგი შეიცავს a → ვექტორის კოორდინატებს, ხოლო მესამე. არის b → ვექტორის კოორდინატები მოცემულ მართკუთხა კოორდინატულ სისტემაში, ეს მატრიცის განმსაზღვრელი ასე გამოიყურება: c → = a → × b → = i → j → k → a x a y a z b x b y b z

ამ განმსაზღვრელი პირველი რიგის ელემენტებზე გავაფართოვოთ, მივიღებთ ტოლობას: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b = → a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

ჯვარედინი პროდუქტის თვისებები

ცნობილია, რომ ვექტორული ნამრავლი კოორდინატებში წარმოდგენილია c → = a → × b → = i → j → k → a x a y a z b x b y b z მატრიცის განმსაზღვრელი, შემდეგ ფუძეზე. მატრიცის განმსაზღვრელი თვისებებიშემდეგი ვექტორული პროდუქტის თვისებები:

1. ანტიკომუტატიურობა a → × b → = - b → × a →;
2. განაწილება a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → ან a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. ასოციაციურობა λ a → × b → = λ a → × b → ან a → × (λ b →) = λ a → × b → , სადაც λ არის თვითნებური რეალური რიცხვი.

ამ თვისებებს არ გააჩნია რთული მტკიცებულებები.

მაგალითად, ჩვენ შეგვიძლია დავამტკიცოთ ვექტორული პროდუქტის ანტიკომუტატიურობის თვისება.

ანტიკომუტატიურობის მტკიცებულება

განმარტებით, a → × b → = i → j → k → a x a y a z b x b y b z და b → × a → = i → j → k → b x b y b z a x a y a z. და თუ მატრიცის ორი მწკრივი ერთმანეთს ენაცვლება, მაშინ მატრიცის განმსაზღვრელი მნიშვნელობა უნდა შეიცვალოს საპირისპიროდ, შესაბამისად, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y. - b → × a → , რაც და ადასტურებს ვექტორული ნამრავლის ანტიკომუტატიურობას.

ვექტორული პროდუქტი - მაგალითები და გადაწყვეტილებები

უმეტეს შემთხვევაში, არსებობს სამი სახის დავალება.

პირველი ტიპის ამოცანებში, როგორც წესი, მოცემულია ორი ვექტორის სიგრძე და მათ შორის კუთხე, მაგრამ თქვენ უნდა იპოვოთ ჯვარედინი ნამრავლის სიგრძე. ამ შემთხვევაში გამოიყენეთ შემდეგი ფორმულა c → = a → b → sin ∠ a → , b → .

მაგალითი 1

იპოვეთ a → და b → ვექტორების ჯვარედინი ნამრავლის სიგრძე, თუ ცნობილია a → = 3 , b → = 5 , ∠ a → , b → = π 4.

გამოსავალი

a → და b → ვექტორების ვექტორული ნამრავლის სიგრძის განსაზღვრის გამოყენებით ვხსნით ამ ამოცანას: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

პასუხი: 15 2 2 .

მეორე ტიპის ამოცანებს აქვს კავშირი ვექტორების კოორდინატებთან, შეიცავს ვექტორულ ნამრავლს, მის სიგრძეს და ა.შ. მოძებნა ცნობილი კოორდინატები მოცემული ვექტორები a → = (a x ; a y ; a z) და b → = (b x ; b y ; b z) .

ამ ტიპის ამოცანისთვის შეგიძლიათ ამოცანების მრავალი ვარიანტის გადაჭრა. მაგალითად, არა a → და b → ვექტორების კოორდინატები, არამედ მათი გაფართოებები ფორმის კოორდინატულ ვექტორებში. b → = b x i → + b y j → + b z k → და c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , ან a → და b → ვექტორები შეიძლება მიცემული იყოს მათი კოორდინატებით. საწყისი და დასასრული წერტილები.

განვიხილოთ შემდეგი მაგალითები.

მაგალითი 2

მართკუთხა კოორდინატულ სისტემაში დაყენებულია ორი ვექტორი a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . იპოვეთ მათი ვექტორული პროდუქტი.

გამოსავალი

მეორე განმარტების მიხედვით, მოცემულ კოორდინატებში ვპოულობთ ორი ვექტორის ვექტორულ ნამრავლს: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 კ → .

თუ ვექტორულ ნამრავლს ჩავწერთ მატრიცის განმსაზღვრელი საშუალებით, მაშინ ამ მაგალითის ამოხსნა ასეთია: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

პასუხი: a → × b → = - 2 i → - 2 j → - 2 k →.

მაგალითი 3

იპოვეთ i → - j → და i → + j → + k → ვექტორების ჯვარედინი ნამრავლის სიგრძე, სადაც i → , j → , k → - მართკუთხა დეკარტის კოორდინატთა სისტემის ორტები.

გამოსავალი

ჯერ ვიპოვოთ მოცემული ვექტორული ნამრავლის კოორდინატები i → - j → × i → + j → + k → მოცემულ მართკუთხა კოორდინატულ სისტემაში.

ცნობილია, რომ i → - j → და i → + j → + k → ვექტორებს აქვთ კოორდინატები (1 ; - 1 ; 0) და (1 ; 1 ; 1) შესაბამისად. იპოვეთ ვექტორული ნამრავლის სიგრძე მატრიცის განმსაზღვრელი გამოყენებით, შემდეგ გვაქვს i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 კ → .

ამიტომ ვექტორულ ნამრავლს i → - j → × i → + j → + k → აქვს კოორდინატები (- 1 ; - 1 ; 2) მოცემულ კოორდინატულ სისტემაში.

ვექტორული ნამრავლის სიგრძეს ვპოულობთ ფორმულით (იხ. განყოფილება ვექტორის სიგრძის პოვნის შესახებ): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

პასუხი: i → - j → × i → + j → + k → = 6 . .

მაგალითი 4

სამი წერტილის A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) კოორდინატები მოცემულია მართკუთხა დეკარტის კოორდინატულ სისტემაში. იპოვნეთ A B → და A C → პერპენდიკულარული ვექტორი ერთდროულად.

გამოსავალი

A B → და A C → ვექტორებს აქვთ შემდეგი კოორდინატები (- 1 ; 2 ; 2) და (0 ; 4 ; 1) შესაბამისად. ვიპოვეთ A B → და A C → ვექტორების ვექტორული ნამრავლი, აშკარაა, რომ ის არის პერპენდიკულარული ვექტორი A B → და A C →, ანუ ის არის ჩვენი პრობლემის გადაწყვეტა. იპოვეთ ის A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k →.

პასუხი: - 6 i → + j → - 4 k → . არის ერთ-ერთი პერპენდიკულარული ვექტორი.

მესამე ტიპის ამოცანები ფოკუსირებულია ვექტორების ვექტორული ნამრავლის თვისებების გამოყენებაზე. რომლის გამოყენების შემდეგ ჩვენ მივიღებთ მოცემული პრობლემის გადაწყვეტას.

მაგალითი 5

ვექტორები a → და b → პერპენდიკულარულია და მათი სიგრძეა შესაბამისად 3 და 4. იპოვეთ ჯვრის ნამრავლის სიგრძე 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →.

გამოსავალი

ვექტორული ნამრავლის განაწილების თვისებით შეგვიძლია დავწეროთ 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

ასოციაციურობის თვისებით ვიღებთ რიცხვით კოეფიციენტებს ვექტორული ნამრავლების ნიშნის მიღმა ბოლო გამოსახულებაში: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

ვექტორული ნამრავლები a → × a → და b → × b → ტოლია 0-ის, ვინაიდან a → × a → = a → a → sin 0 = 0 და b → × b → = b → b → sin 0 = 0, შემდეგ 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a →. .

ვექტორული ნამრავლის ანტიკომუტატიურობიდან გამომდინარეობს - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

ვექტორული ნამრავლის თვისებების გამოყენებით ვიღებთ ტოლობას 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

პირობით, a → და b → ვექტორები პერპენდიკულარულია, ანუ მათ შორის კუთხე π 2-ის ტოლია. ახლა რჩება მხოლოდ ნაპოვნი მნიშვნელობების შესაბამის ფორმულებში ჩანაცვლება: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

პასუხი: 3 a → - b → × a → - 2 b → = 60 .

ვექტორების ჯვარედინი ნამრავლის სიგრძე განსაზღვრებით არის a → × b → = a → · b → · sin ∠ a → , b →. ვინაიდან უკვე ცნობილია (სასკოლო კურსიდან), რომ სამკუთხედის ფართობი უდრის მისი ორი გვერდის სიგრძის ნამრავლის ნახევარს, გამრავლებული ამ გვერდებს შორის კუთხის სინუსზე. მაშასადამე, ვექტორული ნამრავლის სიგრძე უდრის პარალელოგრამის ფართობს - გაორმაგებული სამკუთხედის, კერძოდ, გვერდების ნამრავლი ვექტორების a → და b → სახით, ერთი წერტილიდან, სინუსზე. მათ შორის კუთხის sin ∠ a → , b → .

ეს არის ვექტორული პროდუქტის გეომეტრიული მნიშვნელობა.

ვექტორული პროდუქტის ფიზიკური მნიშვნელობა

მექანიკაში, ფიზიკის ერთ-ერთ ფილიალში, ვექტორული პროდუქტის წყალობით, შეგიძლიათ განსაზღვროთ ძალის მომენტი სივრცის წერტილთან შედარებით.

განმარტება 3

F → ძალის მომენტში, რომელიც გამოიყენება B წერტილზე, A წერტილის მიმართ ჩვენ გავიგებთ შემდეგ ვექტორულ ნამრავლს A B → × F →.

თუ შეამჩნევთ შეცდომას ტექსტში, მონიშნეთ იგი და დააჭირეთ Ctrl+Enter

ცხადია, ჯვარედინი ნამრავლის შემთხვევაში, მნიშვნელოვანია ვექტორების აღების თანმიმდევრობა, უფრო მეტიც,

ასევე, პირდაპირ განმარტებიდან გამომდინარეობს, რომ ნებისმიერი სკალარული ფაქტორის k (რიცხვი) მართებულია შემდეგი:

კოლინარული ვექტორების ჯვარედინი ნამრავლი ნულოვანი ვექტორის ტოლია. უფრო მეტიც, ორი ვექტორის ჯვარედინი ნამრავლი არის ნული, თუ და მხოლოდ იმ შემთხვევაში, თუ ისინი კოლინარულია. (იმ შემთხვევაში, თუ ერთ-ერთი მათგანი ნულოვანი ვექტორია, უნდა გვახსოვდეს, რომ ნულოვანი ვექტორი არის კოლინარული ნებისმიერი ვექტორის განსაზღვრებით).

ვექტორულ პროდუქტს აქვს გამანაწილებელი ქონება, ანუ

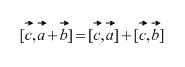
ჯვარედინი ნამრავლის გამოხატულება ვექტორების კოორდინატებში.

მიეცით ორი ვექტორი

(როგორ ვიპოვოთ ვექტორის კოორდინატები მისი დასაწყისისა და დასასრულის კოორდინატების მიხედვით - იხილეთ სტატია ვექტორების წერტილოვანი ნამრავლი, პუნქტი წერტილოვანი ნამრავლის ალტერნატიული განმარტება ან მათი კოორდინატებით მოცემული ორი ვექტორის წერტილოვანი ნამრავლის გამოთვლა.)

რატომ გჭირდებათ ვექტორული პროდუქტი?

ჯვარედინი ნამრავლის გამოყენების მრავალი გზა არსებობს, მაგალითად, როგორც უკვე დავწერე ზემოთ, ორი ვექტორის ჯვარედინი ნამრავლის გამოთვლით, შეგიძლიათ გაარკვიოთ, არის თუ არა ისინი კოლინარული.

ან ის შეიძლება გამოყენებულ იქნას როგორც ამ ვექტორებიდან აგებული პარალელოგრამის ფართობის გამოსათვლელად. განმარტებიდან გამომდინარე, მიღებული ვექტორის სიგრძე არის ამ პარალელოგრამის ფართობი.

ასევე დიდი თანხააპლიკაციები არსებობს ელექტროენერგიასა და მაგნიტიზმში.

ვექტორული პროდუქტის ონლაინ კალკულატორი.

ამ კალკულატორის გამოყენებით ორი ვექტორის სკალარული ნამრავლის საპოვნელად, პირველ რიგში უნდა შეიყვანოთ პირველი ვექტორის კოორდინატები, მეორე - მეორე. ვექტორების კოორდინატები შეიძლება გამოითვალოს მათი საწყისი და დასასრული კოორდინატებიდან (იხილეთ სტატია ვექტორების წერტილოვანი ნამრავლი , პუნქტი წერტილოვანი ნამრავლის ალტერნატიული განმარტება, ან ორი ვექტორის წერტილოვანი ნამრავლის გამოთვლა მათი კოორდინატების გათვალისწინებით.)