Vektorski proizvod vektora u prostoru. vektorski proizvod

Očigledno, u slučaju unakrsnog proizvoda, poredak kojim se uzimaju vektori bitan, štaviše,

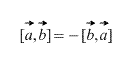
Takođe, direktno iz definicije sledi da je za bilo koji skalarni faktor k (broj) tačno sledeće:

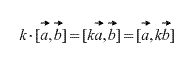
Unakrsni proizvod kolinearnih vektora jednak je nultom vektoru. Nadalje, vektorski proizvod dva vektora su nula ako i samo ako su kolinearni. (U slučaju da je jedan od njih nulti vektor potrebno je zapamtiti da je nulti vektor kolinearan bilo kojem vektoru po definiciji).

Vektorski proizvod ima distributivna svojina, to je

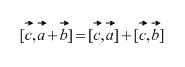
Izraz unakrsnog proizvoda u terminima koordinata vektora.

Neka su data dva vektora

(kako pronaći koordinate vektora po koordinatama njegovog početka i kraja - pogledajte članak Tačkasti proizvod vektora, paragraf Alternativna definicija tačkastog proizvoda ili izračunavanje tačkastog proizvoda dva vektora datih njihovim koordinatama.)

Zašto vam je potreban vektorski proizvod?

Postoji mnogo načina da se koristi unakrsni proizvod, na primjer, kao što je već napisano gore, izračunavanjem unakrsnog proizvoda dva vektora možete saznati jesu li kolinearni.

Ili se može koristiti kao način za izračunavanje površine paralelograma izgrađenog od ovih vektora. Na osnovu definicije, dužina rezultirajućeg vektora je površina ovog paralelograma.

Također velika količina primjene postoje u elektricitetu i magnetizmu.

Online kalkulator vektorskog proizvoda.

Da biste pronašli skalarni proizvod dva vektora pomoću ovog kalkulatora, morate u prvi red unijeti koordinate prvog vektora, u drugi - drugi. Koordinate vektora mogu se izračunati iz njihovih početnih i krajnjih koordinata (vidi članak Tačkasti proizvod vektora , stavka Alternativna definicija dot proizvoda, ili izračunavanje dot proizvoda dva vektora s obzirom na njihove koordinate.)

Definicija. Vektorski umnožak vektora a (množitelja) sa vektorom (množiteljem) koji mu nije kolinearan je treći vektor c (proizvod), koji se konstruiše na sljedeći način:

1) njegov modul je numerički jednak površini paralelograma na sl. 155), izgrađen na vektorima, odnosno jednak je pravcu okomitom na ravan pomenutog paralelograma;

3) u ovom slučaju se bira pravac vektora c (od dva moguća) tako da vektori c formiraju desnoruki sistem (§ 110).

Oznaka: ili

Dodatak definiciji. Ako su vektori kolinearni, smatrajući figuru (uslovno) paralelogramom, prirodno je dodijeliti nultu površinu. Stoga se vektorski proizvod kolinearnih vektora smatra jednakim nultom vektoru.

Pošto se nultom vektoru može dodijeliti bilo koji smjer, ova konvencija nije u suprotnosti sa stavkama 2 i 3 definicije.

Napomena 1. U terminu "vektorski proizvod", prva riječ označava da je rezultat akcije vektor (za razliku od skalarnog proizvoda; up. § 104, napomena 1).

Primjer 1. Pronađite vektorski proizvod gdje su glavni vektori desnog koordinatnog sistema (Sl. 156).

1. Pošto su dužine glavnih vektora jednake jedinici skale, površina paralelograma (kvadrata) je brojčano jednaka jedan. Dakle, modul vektorskog proizvoda jednak je jedan.

2. Pošto je okomita na ravan osa, željeni vektorski proizvod je vektor kolinearan vektoru k; a pošto oba imaju modul 1, traženi unakrsni proizvod je ili k ili -k.

3. Od ova dva moguća vektora, mora se izabrati prvi, pošto vektori k formiraju desni sistem (a vektori levi).

Primjer 2. Pronađite unakrsni proizvod

Rješenje. Kao u primjeru 1, zaključujemo da je vektor ili k ili -k. Ali sada moramo izabrati -k, pošto vektori formiraju desni sistem (a vektori čine levi). dakle,

Primjer 3 Vektori imaju dužine od 80 i 50 cm, respektivno, i formiraju ugao od 30°. Uzimajući metar kao jedinicu dužine, pronađite dužinu vektorskog proizvoda a

Rješenje. Površina paralelograma izgrađenog na vektorima je jednaka Dužina željenog vektorskog proizvoda jednaka je

Primjer 4. Odrediti dužinu poprečnog proizvoda istih vektora, uzimajući centimetar kao jedinicu dužine.

Rješenje. Pošto je površina paralelograma izgrađenog na vektorima jednaka dužini vektorskog proizvoda 2000 cm, tj.

Poređenje primjera 3 i 4 pokazuje da dužina vektora ne zavisi samo od dužina faktora, već i od izbora jedinice dužine.

Fizičko značenje vektorskog proizvoda. Od mnogih fizičkih veličina predstavljenih vektorskim proizvodom, razmotrit ćemo samo moment sile.

Neka je A tačka primene sile. Moment sile u odnosu na tačku O naziva se vektorski proizvod. Pošto je modul ovog vektorskog proizvoda brojčano jednak površini paralelograma (Sl. 157), Modul momenta jednak je umnošku baze na visinu, tj. sili pomnoženoj sa rastojanjem od tačke O do prave linije duž koje sila deluje.

U mehanici je dokazano da je za ravnotežu krutog tijela potrebno da ne samo zbir vektora koji predstavljaju sile primijenjene na tijelo, već i zbir momenata sila bude jednak nuli. U slučaju kada su sve sile paralelne sa istom ravninom, sabiranje vektora koji predstavljaju momente može se zamijeniti sabiranjem i oduzimanjem njihovih modula. Ali za proizvoljne smjerove sila, takva zamjena je nemoguća. U skladu s tim, unakrsni proizvod je definiran upravo kao vektor, a ne kao broj.

Definicija. Vektorski proizvod vektora a i vektora b je vektor označen simbolom [«, b] (ili l x b), takav da je 1) dužina vektora [a, b] jednaka (p, gdje je y ugao između vektora a i b ( 31); 2) vektor [a, b) je okomit na vektore a i b, tj. okomito na ravan ovih vektora; 3) vektor [a, b] je usmjeren tako da se od kraja ovog vektora vidi da se najkraći zaokret od a do b odvija u smjeru suprotnom od kazaljke na satu (slika 32). Rice. 32 Sl.31 Drugim riječima, vektori a, b i [a, b) čine desnu trojku vektora, tj. koji se nalaze kao palac, kažiprst i srednji prst desne ruke. Ako su vektori a i b kolinearni, pretpostavićemo da je [a, b] = 0. Po definiciji, dužina vektorskog proizvoda je brojčano jednaka površini Sa paralelograma (slika 33) izgrađenog na pomnoženim vektorima a i b kao na stranama: 6.1. Svojstva vektorskog proizvoda 1. Vektorski proizvod je jednak nultom vektoru ako i samo ako je barem jedan od pomnoženih vektora nula ili kada su ovi vektori kolinearni (ako su vektori a i b kolinearni, tada je ugao između njih je ili 0 ili 7r). Ovo je lako dobiti iz činjenice da ako uzmemo u obzir nulti vektor kolinsar bilo kojem vektoru, onda se uslov kolinarnosti vektora a i b može izraziti na sljedeći način 2. Vektorski proizvod je antikomutativan, tj. uvijek. Zaista, vektori (a, b) i imaju istu dužinu i kolinearni su. Smjerovi ovih vektora su suprotni, jer će se od kraja vektora [a, b] vidjeti najkraći zaokret od a do b u smjeru suprotnom od kazaljke na satu, a od kraja vektora [b, a] - u smjeru kazaljke na satu (Sl. 34). 3. Vektorski proizvod ima distributivno svojstvo u odnosu na sabiranje 4. Numerički faktor A može se izvaditi iz predznaka vektorskog proizvoda 6.2. Vektorski proizvod vektora datih koordinatama Neka su vektori a i b dati svojim koordinatama u bazi. Koristeći svojstvo distribucije vektorskog proizvoda, nalazimo vektorski proizvod vektora datih koordinatama. Mješoviti posao. Zapišimo vektorske produkte koordinatnih orta (slika 35): Dakle, za vektorski proizvod vektora a i b, iz formule (3) dobijamo sljedeću determinantu izraza nad elementima 1. reda, dobijamo ( 4). Primjeri. 1. Pronađite površinu paralelograma izgrađenog na vektorima Nađite površinu trokuta (slika 36). Jasno je da je površina b "d trokuta JSC jednaka polovini površine S paralelograma O AC B. Izračunavanje vektorskog proizvoda (a, b | vektora a = OA i b = b = ob ), dobijamo (a, b), c) = [a, |b, c)) nije tačno u opštem slučaju. Na primer, za a = ss j imamo § 7. Mješoviti proizvod vektora Neka imamo tri vektora a, b i c. Vektore a i 1> pomnožimo vektorski. Kao rezultat dobijamo vektor [a, 1>]. Pomnožimo ga skalarno vektorom c: (k b), c. Broj ( [a, b], e) naziva se mješoviti proizvod vektora a, b. c i označava se simbolom (a, 1), e. 7.1 Geometrijsko značenje mješovitog proizvoda Ostavimo vektore a, b i iz opšte tačke O (slika 37). Ako sve četiri tačke O, A, B, C leže u istoj ravni (vektori a, b i c se u ovom slučaju nazivaju komplanarni), tada se mješoviti proizvod ([a, b], c) = 0. Ovo proizilazi iz činjenice da je vektor [a, b| okomit na ravan u kojoj leže vektori a i 1", a time i vektor c. / Ako je t tačke O, A, B, C ne leže u istoj ravni (vektori a, b i c su nekoplanarni), izgradićemo paralelepiped na ivicama OA, OB i OS (sl. 38 a). Prema definiciji unakrsnog proizvoda, imamo (a,b) = So c, gdje je So površina paralelograma OADB, a c je jedinični vektor okomit na vektore a i b i takav da je trojka a , b, c je u pravu, tj. vektori a, b i c nalaze se redom kao palac, kažiprst i srednji prst desne ruke (slika 38 b). Množenjem oba dijela posljednje jednakosti na desnom skalaru vektorom c dobijamo da je vektorski proizvod vektora datih koordinatama. Mješoviti posao. Broj rc c jednak je visini h konstruisanog paralelepipeda, uzet sa znakom “+” ako je ugao između vektora c i c oštar (trojka a, b, c je prava), i sa predznakom “ -” ako je ugao tup (trojka a, b, c - lijevo), tako da je mješoviti proizvod vektora a, b i c jednak volumenu V paralelepipeda izgrađenog na ovim vektorima kao na rubovima ako je trojka a, b, c desna, i -V ako je trojka a, b, c - lijevo. Na osnovu geometrijskog značenja mješovitog proizvoda, možemo zaključiti da ćemo množenjem istih vektora a, b i c bilo kojim drugim redom uvijek dobiti ili +7 ili -K. Znak pro- Sl. 38 referenca će zavisiti samo od toga koji triplet formiraju pomnoženi vektori - desni ili levi. Ako vektori a, b, c formiraju desnu trojku, tada će i trojke b, c, a i c, a, b također biti ispravne. Istovremeno, sve tri trojke b, a, c; a, c, b i c, b, a - lijevo. Dakle, (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b, a). Još jednom naglašavamo da je mješoviti proizvod vektora jednak nuli ako i samo ako su pomnoženi vektori a, b, c koplanarni: (a, b, c su koplanarni) 7.2. Mješoviti proizvod u koordinatama Neka su vektori a, b, c dati svojim koordinatama u bazi i, j, k: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Nađimo izraz za njihov mješoviti proizvod (a, b, c). Imamo mješoviti proizvod vektora datih njihovim koordinatama u bazi i, J, k, jednak determinanti trećeg reda, čije su linije sastavljene od koordinata prvog, drugog i trećeg pomnoženog vektori. Neophodan i dovoljan uslov za komplanarnost vektora a y\, Z|), b = (xx, y2.22), c = (x3, uz, 23) može se zapisati u sledećem obliku z, ar2 y2 -2 =0. Uz Primjer. Provjerite jesu li vektori v = (7,4,6), b = (2, 1,1), c = (19, II, 17) koplanarni. Vektori koji se razmatraju biće komplanarni ili nekoplanarni, u zavisnosti od toga da li je determinanta jednaka nuli ili ne. Proširujući je u smislu elemenata prvog reda, dobijamo 7.3. Dvostruki unakrsni proizvod Dvostruki unakrsni proizvod [a, [b, c]] je vektor okomit na vektore a i [b, c]. Stoga leži u ravni vektora b i c i može se proširiti u ove vektore. Može se pokazati da je formula [a, [!>, c]] = b(a, e) - c(a, b) važeća. Vježbe 1. Tri vektora AB = c, W? = o i CA = b služe kao stranice trougla. Izrazite u terminima a, b i c vektore koji se poklapaju sa medijanima AM, DN, CP trougla. 2. Koji uslov mora biti povezan između vektora p i q tako da vektor p + q podijeli ugao između njih na pola? Pretpostavlja se da su sva tri vektora povezana sa zajedničkim poreklom. 3. Izračunajte dužinu dijagonala paralelograma izgrađenog na vektorima a = 5p + 2q i b = p - 3q, ako je poznato da je |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Označavajući sa a i b stranice romba koje izlaze iz zajedničkog vrha, dokazati da su dijagonale romba međusobno okomite. 5. Izračunajte dot proizvod vektora a = 4i + 7j + 3k i b = 31 - 5j + k. 6. Pronađite jedinični vektor a0 paralelan vektoru a = (6, 7, -6). 7. Pronađite projekciju vektora a = l+ j- kHa vektora b = 21 - j - 3k. 8. Naći kosinus ugla između vektora IS "w, ako je A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Pronađite jedinični vektor p° koji je istovremeno okomit na vektor a = (3, 6, 8) i x-osu. 10. Izračunajte sinus ugla između dijagonala paralelofama izgrađenog na vektorima a = 2i+J-k, b=i-3j + k kao na stranicama. Izračunajte visinu h paralelepipeda izgrađenog na vektorima a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k, ako se za osnovu uzme paralelogram izgrađen na vektorima a i I). Odgovori

Prije nego damo pojam vektorskog proizvoda, osvrnimo se na pitanje orijentacije uređene trojke vektora a → , b → , c → u trodimenzionalnom prostoru.

Za početak, odvojimo vektore a → , b → , c → iz jedne tačke. Orijentacija trojke a → , b → , c → je desna ili lijeva, ovisno o smjeru vektora c → . Iz smjera u kojem se pravi najkraći okret od vektora a → do b → od kraja vektora c → , odredit će se oblik trojke a → , b → , c →.

Ako je najkraća rotacija u smjeru suprotnom od kazaljke na satu, tada se trojka vektora a → , b → , c → naziva u pravu ako u smjeru kazaljke na satu - lijevo.

Sledeće, uzmi dva kolinearni vektori a → i b → . Odložimo tada vektore A B → = a → i A C → = b → iz tačke A. Konstruirajmo vektor A D → = c → , koji je istovremeno okomit i na A B → i na A C → . Dakle, kada konstruišemo vektor A D → = c →, možemo uraditi dve stvari, dajući mu ili jedan ili suprotan smer (vidi ilustraciju).

Uređeni trio vektora a → , b → , c → može biti, kako smo saznali, desni ili levi u zavisnosti od smera vektora.

Iz navedenog možemo uvesti definiciju vektorskog proizvoda. Ova definicija je data za dva vektora definisana u pravougaonom koordinatnom sistemu trodimenzionalnog prostora.

Definicija 1

Vektorski proizvod dva vektora a → i b → nazvaćemo takav vektor dat u pravougaonom koordinatnom sistemu trodimenzionalnog prostora tako da:

ako su vektori a → i b → kolinearni, biće nula;
bit će okomit na vektor a → i vektor b → tj. ∠ a → c → = ∠ b → c → = π 2 ;
njegova dužina je određena formulom: c → = a → b → sin ∠ a → , b → ;
triplet vektora a → , b → , c → ima istu orijentaciju kao dati koordinatni sistem.

Unakrsni proizvod vektora a → i b → ima sljedeću notaciju: a → × b → .

Unakrsne koordinate proizvoda

Pošto svaki vektor ima određene koordinate u koordinatnom sistemu, moguće je uvesti drugu definiciju vektorskog proizvoda, koja će vam omogućiti da pronađete njegove koordinate iz datih koordinata vektora.

Definicija 2

U pravougaonom koordinatnom sistemu trodimenzionalnog prostora vektorski proizvod dva vektora a → = (a x ; a y ; a z) i b → = (b x ; b y ; b z) nazovimo vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , gdje su i → , j → , k → koordinatni vektori.

Vektorski proizvod se može predstaviti kao determinanta kvadratne matrice trećeg reda, gdje su prvi red orta vektori i → , j → , k → , drugi red sadrži koordinate vektora a → , a treći je koordinate vektora b → u datom pravokutnom koordinatnom sistemu, ova determinanta matrice izgleda ovako: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Proširujući ovu determinantu preko elemenata prvog reda, dobijamo jednakost: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = ( a → × b → = a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Unakrsna svojstva proizvoda

Poznato je da je vektorski proizvod u koordinatama predstavljen kao determinanta matrice c → = a → × b → = i → j → k → a x a y a z b x b y b z , a zatim na bazi svojstva determinante matrice sljedeće svojstva vektorskog proizvoda:

antikomutativnost a → × b → = - b → × a → ;
distributivnost a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → ili a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
asocijativnost λ a → × b → = λ a → × b → ili a → × (λ b →) = λ a → × b → , gdje je λ proizvoljan realan broj.

Ova svojstva nemaju komplikovane dokaze.

Na primjer, možemo dokazati svojstvo antikomutativnosti vektorskog proizvoda.

Dokaz antikomutativnosti

Po definiciji, a → × b → = i → j → k → a x a y a z b x b y b z i b → × a → = i → j → k → b x b y b z a x a y a z . A ako se dva reda matrice zamijene, tada bi se vrijednost determinante matrice trebala promijeniti u suprotno, dakle, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , što i dokazuje antikomutativnost vektorskog proizvoda.

Vektorski proizvod - Primjeri i rješenja

U većini slučajeva postoje tri vrste zadataka.

U problemima prvog tipa obično su date dužine dva vektora i ugao između njih, ali morate pronaći dužinu unakrsnog proizvoda. U ovom slučaju koristite sljedeću formulu c → = a → b → sin ∠ a → , b → .

Primjer 1

Pronađite dužinu unakrsnog proizvoda vektora a → i b → ako je poznato a → = 3, b → = 5, ∠ a →, b → = π 4.

Rješenje

Koristeći definiciju dužine vektorskog proizvoda vektora a → i b →, rješavamo ovaj problem: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

odgovor: 15 2 2 .

Zadaci drugog tipa imaju vezu sa koordinatama vektora, sadrže vektorski proizvod, njegovu dužinu itd. pretraživali po poznatim koordinatama dati vektori a → = (a x ; a y ; a z) i b → = (b x ; b y ; b z) .

Za ovu vrstu zadatka možete riješiti mnogo opcija za zadatke. Na primjer, ne koordinate vektora a → i b → , već njihove ekspanzije u koordinatnim vektorima oblika b → = b x i → + b y j → + b z k → i c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , ili vektori a → i b → mogu biti dati koordinatama njihovih početne i krajnje tačke.

Razmotrite sljedeće primjere.

Primjer 2

Dva vektora postavljena su u pravougaoni koordinatni sistem a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) . Pronađite njihov vektorski proizvod.

Rješenje

Prema drugoj definiciji, nalazimo vektorski proizvod dva vektora u date koordinate: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + (( - 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

Ako vektorski proizvod zapišemo kroz determinantu matrice, rješenje ovog primjera je sljedeće: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

odgovor: a → × b → = - 2 i → - 2 j → - 2 k → .

Primjer 3

Odrediti dužinu unakrsnog proizvoda vektora i → - j → i i → + j → + k → , gdje je i → , j → , k → - orti pravokutnog Dekartovog koordinatnog sistema.

Rješenje

Prvo, pronađimo koordinate datog vektorskog proizvoda i → - j → × i → + j → + k → u datom pravougaonom koordinatnom sistemu.

Poznato je da vektori i → - j → i i → + j → + k → imaju koordinate (1 ; - 1 ; 0) i (1 ; 1 ; 1) respektivno. Nađite dužinu vektorskog proizvoda koristeći determinantu matrice, tada imamo i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Dakle, vektorski proizvod i → - j → × i → + j → + k → ima koordinate (- 1 ; - 1 ; 2) u datom koordinatnom sistemu.

Dužinu vektorskog proizvoda nalazimo po formuli (pogledajte dio o pronalaženju dužine vektora): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

odgovor: i → - j → × i → + j → + k → = 6 . .

Primjer 4

Koordinate tri tačke A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) date su u pravougaonom Dekartovom koordinatnom sistemu. Nađite vektor okomit na A B → i A C → u isto vrijeme.

Rješenje

Vektori A B → i A C → imaju sljedeće koordinate (- 1 ; 2 ; 2) i (0 ; 4 ; 1) redom. Nakon što smo pronašli vektorski proizvod vektora A B → i A C → , očigledno je da je to okomit vektor po definiciji i na A B → i na A C → , odnosno da je rješenje našeg problema. Pronađite ga A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

odgovor: - 6 i → + j → - 4 k → . je jedan od okomitih vektora.

Problemi trećeg tipa fokusirani su na korištenje svojstava vektorskog proizvoda vektora. Nakon primjene koje, dobićemo rješenje zadatog problema.

Primjer 5

Vektori a → i b → su okomiti i njihove dužine su 3 odnosno 4. Pronađite dužinu unakrsnog proizvoda 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Rješenje

Po svojstvu distributivnosti vektorskog proizvoda možemo napisati 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Svojstvom asocijativnosti uzimamo numeričke koeficijente izvan predznaka vektorskih proizvoda u posljednjem izrazu: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektorski proizvodi a → × a → i b → × b → jednaki su 0, budući da su a → × a → = a → a → sin 0 = 0 i b → × b → = b → b → sin 0 = 0 , onda 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

Iz antikomutativnosti vektorskog proizvoda slijedi - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Koristeći svojstva vektorskog proizvoda, dobijamo jednakost 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Pod uslovom, vektori a → i b → su okomiti, odnosno ugao između njih jednak je π 2 . Sada ostaje samo zamijeniti pronađene vrijednosti u odgovarajuće formule: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

odgovor: 3 a → - b → × a → - 2 b → = 60 .

Dužina unakrsnog proizvoda vektora po definiciji je a → × b → = a → · b → · sin ∠ a → , b → . Pošto je već poznato (iz školskog predmeta) da je površina trokuta jednaka polovini umnoška dužina njegovih dviju stranica pomnoženog sa sinusom ugla između ovih stranica. Dakle, dužina vektorskog proizvoda jednaka je površini paralelograma - udvojenog trokuta, odnosno proizvodu stranica u obliku vektora a → i b → , odloženih iz jedne tačke, sinusom ugla između njih sin ∠ a → , b → .

Ovo je geometrijsko značenje vektorskog proizvoda.

Fizičko značenje vektorskog proizvoda

U mehanici, jednoj od grana fizike, zahvaljujući vektorskom proizvodu, možete odrediti moment sile u odnosu na tačku u prostoru.

Definicija 3

Pod momentom sile F → , primenjenom na tačku B, u odnosu na tačku A razumećemo sledeći vektorski proizvod A B → × F → .

Ako primijetite grešku u tekstu, označite je i pritisnite Ctrl+Enter

Svojstva točkastih proizvoda

Skalarni proizvod vektori, definicija, svojstva

Linearne operacije nad vektorima.

Vektori, osnovni pojmovi, definicije, linearne operacije nad njima

Vektor na ravni je uređeni par njegovih tačaka, dok se prva tačka naziva početak, a druga kraj - vektora

Dva vektora se nazivaju jednaka ako su jednaka i kosmjerna.

Vektori koji leže na istoj liniji nazivaju se kosmjernim ako su kosmjerni s nekim od istog vektora koji ne leži na ovoj pravoj.

Vektori koji leže na istoj liniji ili na paralelnim linijama nazivaju se kolinearni, a kolinearni, ali nisu kosmjerni nazivaju se suprotno usmjereni.

Vektori koji leže na okomitim linijama nazivaju se ortogonalni.

Definicija 5.4. suma a+b vektori a i b naziva se vektor koji dolazi od početka vektora a do kraja vektora b , ako je početak vektora b poklapa se sa krajem vektora a .

Definicija 5.5. razlika a - b vektori a i b takav vektor se zove With , koji zajedno sa vektorom b daje vektor a .

Definicija 5.6. radk a vektor a po broju k zove vektor b , kolinearni vektor a , koji ima modul jednak | k||a |, i smjer koji je isti kao i smjer a at k>0 i suprotno a at k<0.

Svojstva množenja vektora brojem:

Nekretnina 1. k(a+b ) = k a+ k b.

Nekretnina 2. (k+m)a = k a+ m a.

Nekretnina 3. k(m a) = (km)a .

Posljedica. Ako su vektori različiti od nule a i b su kolinearni, onda postoji broj k, šta b= k a.

Skalarni proizvod dva vektora različita od nule a i b naziva se broj (skalar) jednak proizvodu dužina ovih vektora i kosinusa ugla φ između njih. Skalarni proizvod se može izraziti na različite načine, na primjer, kao ab, a · b, (a , b), (a · b). Dakle, tačkasti proizvod je:

a · b = |a| · | b| cos φ

Ako je barem jedan od vektora jednak nuli, tada je skalarni proizvod jednak nuli.

Permutacijsko svojstvo: a · b = b · a(skalarni proizvod se ne mijenja permutacijom faktora);

distributivna imovina: a · ( b · c) = (a · b) · c(rezultat ne zavisi od redosleda množenja);

Svojstvo kombinacije (u odnosu na skalarni faktor): (λ a) · b = λ ( a · b).

Svojstvo ortogonalnosti (perpendikularnosti): ako je vektor a i b različiti od nule, tada je njihov proizvod tačaka nula samo kada su ovi vektori ortogonalni (okomiti jedan na drugi) a ┴ b;

Kvadratno svojstvo: a · a = a 2 = |a| 2 (skalarni proizvod vektora sa samim sobom jednak je kvadratu njegovog modula);

Ako su koordinate vektora a=(x 1 , y 1 , z 1 ) i b=(x 2 , y 2 , z 2 ), tada je skalarni proizvod a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .

Vektor drži vektore. Definicija: Vektorski proizvod dva vektora i podrazumijeva se kao vektor za koji:

Modul je jednak površini paralelograma izgrađenog na ovim vektorima, tj. , gdje je ugao između vektora i

Ovaj vektor je okomit na pomnožene vektore, tj.

Ako vektori nisu kolinearni, onda formiraju desnu trojku vektora.

Unakrsna svojstva proizvoda:

1. Kada se promijeni redoslijed faktora, vektorski proizvod mijenja svoj predznak u suprotan, zadržavajući modul, tj.

2 .Vektorski kvadrat je jednak nultom vektoru, tj.

3 .Skalarni faktor se može izvaditi iz predznaka vektorskog proizvoda, tj.

4 .Za bilo koja tri vektora, jednakost

5 .Neophodan i dovoljan uslov za kolinearnost dva vektora i :