Vektorprodukt von Vektoren im Raum. Vektorprodukt

Offensichtlich ist im Fall eines Kreuzprodukts außerdem die Reihenfolge wichtig, in der die Vektoren genommen werden,

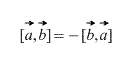
Außerdem folgt direkt aus der Definition, dass für jeden Skalarfaktor k (Zahl) Folgendes gilt:

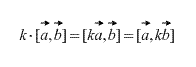
Das Kreuzprodukt kollinearer Vektoren ist gleich dem Nullvektor. Außerdem, Vektorprodukt zwei Vektoren ist genau dann Null, wenn sie kollinear sind. (Falls einer von ihnen ein Nullvektor ist, muss daran erinnert werden, dass der Nullvektor per Definition kollinear zu jedem Vektor ist).

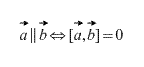
Vektorprodukt hat Verteilungseigenschaft, also

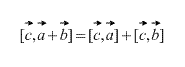
Der Ausdruck des Kreuzprodukts in Bezug auf die Koordinaten der Vektoren.

Gegeben seien zwei Vektoren

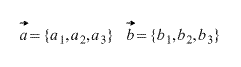
(wie man die Koordinaten eines Vektors anhand der Koordinaten seines Anfangs und Endes findet - siehe Artikel Skalarprodukt von Vektoren, Abschnitt Alternative Definition des Skalarprodukts oder Berechnung des Skalarprodukts zweier Vektoren, die durch ihre Koordinaten gegeben sind. )

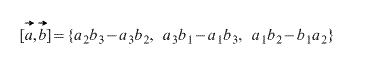
Warum brauchen Sie ein Vektorprodukt?

Es gibt viele Möglichkeiten, das Kreuzprodukt zu verwenden, zum Beispiel, wie oben bereits geschrieben, indem Sie das Kreuzprodukt zweier Vektoren berechnen, können Sie herausfinden, ob sie kollinear sind.

Oder es kann verwendet werden, um die Fläche eines aus diesen Vektoren erstellten Parallelogramms zu berechnen. Aufgrund der Definition ist die Länge des resultierenden Vektors die Fläche dieses Parallelogramms.

Ebenfalls große Menge Anwendungen gibt es in Elektrizität und Magnetismus.

Online-Rechner des Vektorprodukts.

Um mit diesem Rechner das Skalarprodukt zweier Vektoren zu ermitteln, müssen Sie in der ersten Zeile die Koordinaten des ersten Vektors in eingeben zweite - zweite. Die Koordinaten von Vektoren können aus ihren Start- und Endkoordinaten berechnet werden (siehe Artikel Skalarprodukt von Vektoren , Punkt Eine alternative Definition des Skalarprodukts oder die Berechnung des Skalarprodukts zweier Vektoren anhand ihrer Koordinaten.)

Definition. Das Vektorprodukt eines Vektors a (Multiplikator) mit einem nicht kollinearen Vektor (Multiplikator) ist der dritte Vektor c (Produkt), der wie folgt aufgebaut ist:

1) sein Modul ist numerisch gleich der Fläche des Parallelogramms in Abb. 155), auf Vektoren aufgebaut, d.h. es ist gleich der Richtung senkrecht zur Ebene des erwähnten Parallelogramms;

3) In diesem Fall wird die Richtung des Vektors c (aus zwei möglichen) so gewählt, dass die Vektoren c ein rechtshändiges System bilden (§ 110).

Bezeichnung: bzw

Ergänzung zur Definition. Wenn die Vektoren kollinear sind und die Figur als (bedingtes) Parallelogramm betrachtet wird, ist es natürlich, eine Nullfläche zuzuweisen. Daher wird das Vektorprodukt kollinearer Vektoren als gleich dem Nullvektor betrachtet.

Da dem Nullvektor jede Richtung zugeordnet werden kann, widerspricht diese Konvention nicht den Punkten 2 und 3 der Definition.

Bemerkung 1. Im Begriff "Vektorprodukt" weist das erste Wort darauf hin, dass das Ergebnis einer Aktion ein Vektor ist (im Gegensatz zu einem Skalarprodukt; vgl. § 104, Bemerkung 1).

Beispiel 1. Finden Sie das Vektorprodukt, wo die Hauptvektoren des rechten Koordinatensystems (Abb. 156).

1. Da die Längen der Hauptvektoren gleich der Skaleneinheit sind, ist die Fläche des Parallelogramms (Quadrat) numerisch gleich eins. Daher ist der Modul des Vektorprodukts gleich eins.

2. Da die Senkrechte zur Ebene die Achse ist, ist das gewünschte Vektorprodukt ein Vektor, der kollinear zum Vektor k ist; und da beide Modul 1 haben, ist das erforderliche Kreuzprodukt entweder k oder -k.

3. Von diesen beiden möglichen Vektoren muss der erste gewählt werden, da die Vektoren k ein rechtes System bilden (und die Vektoren ein linkes).

Beispiel 2. Finden Sie das Kreuzprodukt

Lösung. Wie in Beispiel 1 schließen wir daraus, dass der Vektor entweder k oder -k ist. Aber jetzt müssen wir -k wählen, da die Vektoren das rechte System bilden (und die Vektoren das linke). So,

Beispiel 3 Die Vektoren haben eine Länge von 80 bzw. 50 cm und bilden einen Winkel von 30°. Nimm einen Meter als Längeneinheit und bestimme die Länge des Vektorprodukts a

Lösung. Die Fläche eines auf Vektoren aufgebauten Parallelogramms ist gleich Die Länge des gewünschten Vektorprodukts ist gleich

Beispiel 4. Ermitteln Sie die Länge des Kreuzprodukts derselben Vektoren, indem Sie einen Zentimeter als Längeneinheit nehmen.

Lösung. Da die Fläche des auf Vektoren aufgebauten Parallelogramms gleich der Länge des Vektorprodukts ist, beträgt 2000 cm, d.h.

Der Vergleich der Beispiele 3 und 4 zeigt, dass die Länge des Vektors nicht nur von den Längen der Faktoren abhängt, sondern auch von der Wahl der Längeneinheit.

Die physikalische Bedeutung des Vektorprodukts. Von den vielen physikalischen Größen, die durch das Vektorprodukt dargestellt werden, betrachten wir nur das Moment der Kraft.

Sei A der Angriffspunkt der Kraft. Das Kraftmoment relativ zum Punkt O wird als Vektorprodukt bezeichnet. Da das Modul dieses Vektorprodukts numerisch gleich der Fläche des Parallelogramms ist (Abb. 157), Der Momentenmodul ist gleich dem Produkt aus der Basis und der Höhe, d. h. der Kraft multipliziert mit dem Abstand vom Punkt O zur geraden Linie, entlang der die Kraft wirkt.

In der Mechanik ist bewiesen, dass für das Gleichgewicht eines starren Körpers nicht nur die Summe der Vektoren, die die auf den Körper wirkenden Kräfte darstellen, sondern auch die Summe der Kraftmomente gleich Null sein muss. Wenn alle Kräfte parallel zu derselben Ebene sind, kann die Addition der Vektoren, die die Momente darstellen, durch die Addition und Subtraktion ihrer Beträge ersetzt werden. Aber für beliebige Kraftrichtungen ist eine solche Ersetzung unmöglich. Dementsprechend ist das Kreuzprodukt genau als Vektor und nicht als Zahl definiert.

Definition. Das Vektorprodukt eines Vektors a und eines Vektors b ist ein Vektor, der durch das Symbol [«, b] (oder l x b) bezeichnet wird, so dass 1) die Länge des Vektors [a, b] gleich (p, wobei y ist der Winkel zwischen den Vektoren a und b ( 31); 2) der Vektor [a, b) steht senkrecht auf den Vektoren a und b, d.h. senkrecht zur Ebene dieser Vektoren; 3) Der Vektor [a, b] ist so gerichtet, dass vom Ende dieses Vektors aus gesehen die kürzeste Drehung von a nach b im Gegenuhrzeigersinn erfolgt (Abb. 32). Reis. 32 Abb.31 Mit anderen Worten, die Vektoren a, b und [а, b) bilden das rechte Vektortripel, d.h. befinden sich wie Daumen, Zeige- und Mittelfinger der rechten Hand. Wenn die Vektoren a und b kollinear sind, nehmen wir an, dass [a, b] = 0. Per Definition ist die Länge des Vektorprodukts numerisch gleich der Fläche Sa des Parallelogramms (Abb. 33), das auf den multiplizierten Vektoren aufgebaut ist a und b wie an den Seiten: 6.1 . Eigenschaften eines Vektorprodukts 1. Ein Vektorprodukt ist genau dann gleich einem Nullvektor, wenn mindestens einer der multiplizierten Vektoren Null ist oder wenn diese Vektoren kollinear sind (wenn die Vektoren a und b kollinear sind, dann der Winkel zwischen ihnen ist entweder 0 oder 7r). Dies ergibt sich leicht aus der Tatsache, dass Wenn wir den Nullvektor kollinar zu einem beliebigen Vektor betrachten, dann lässt sich die Bedingung für die Kollinarität der Vektoren a und b wie folgt ausdrücken 2. Das Vektorprodukt ist antikommutativ, also immer. Tatsächlich haben die Vektoren (a, b) und die gleiche Länge und sind kollinear. Die Richtungen dieser Vektoren sind entgegengesetzt, da vom Ende des Vektors [a, b] aus gesehen wird, dass die kürzeste Drehung von a nach b gegen den Uhrzeigersinn erfolgt, und vom Ende des Vektors [b, a] aus im Uhrzeigersinn (Abb. 34). 3. Das Vektorprodukt hat eine Distributiv-Eigenschaft bezüglich der Addition 4. Der Zahlenfaktor A kann aus dem Vorzeichen des Vektorprodukts herausgenommen werden 6.2. Vektorprodukt von durch Koordinaten gegebenen Vektoren Die Vektoren a und b seien durch ihre Koordinaten in der Basis gegeben. Unter Verwendung der Verteilungseigenschaft des Vektorprodukts finden wir das Vektorprodukt der durch die Koordinaten gegebenen Vektoren. Gemischte Arbeit. Schreiben wir die Vektorprodukte der Koordinatenorte aus (Abb. 35): Daher erhalten wir für das Vektorprodukt der Vektoren a und b aus Formel (3) den folgenden Ausdruck Determinante über den Elementen der 1. Reihe erhalten wir ( 4). Beispiele. 1. Finden Sie die Fläche eines Parallelogramms, das auf Vektoren aufgebaut ist Finden Sie die Fläche des Dreiecks (Abb. 36). Es ist klar, dass die Fläche b "d des Dreiecks JSC gleich der Hälfte der Fläche S des Parallelogramms O AC B ist. Berechnung des Vektorprodukts (a, b | der Vektoren a \u003d OA und b \u003d b \u003d ob) erhalten wir (a, b), c) = [a, |b, c)) ist im allgemeinen Fall nicht wahr, zB für a = ss j gilt § 7. Gemischtes Produkt von Vektoren Lassen Sie uns haben drei Vektoren a, b und c. Multiplizieren Sie die Vektoren a und 1> vektoriell. Als Ergebnis erhalten wir den Vektor [a, 1>] Wir multiplizieren ihn skalar mit dem Vektor c: (k b), c. Die Zahl ([a, b], e) heißt gemischtes Produkt der Vektoren a, b, c und wird mit dem Symbol (a, 1), e bezeichnet) 7.1 Die geometrische Bedeutung des gemischten Produkts Lassen Sie uns setzen neben den Vektoren a, b und vom allgemeinen Punkt O (Abb. 37) Liegen alle vier Punkte O, A, B, C in derselben Ebene (die Vektoren a, b und c heißen in diesem Fall koplanar), dann das Mischprodukt ([a, b], c) = 0. Dies folgt daraus, dass der Vektor [a, b| senkrecht auf der Ebene steht, in der die Vektoren a und 1 liegen ", und damit der Vektor c. / Wenn t Da die Punkte O, A, B, C nicht in einer Ebene liegen (die Vektoren a, b und c sind nicht koplanar), konstruieren wir einen Quader auf den Kanten OA, OB und OS (Abb. 38a). Durch die Definition eines Kreuzprodukts haben wir (a,b) = So c, wobei So die Fläche des OADB-Parallelogramms ist und c ein Einheitsvektor ist, der senkrecht zu den Vektoren a und b steht und so dass das Tripel a , b, c ist richtig, d.h. Die Vektoren a, b und c befinden sich jeweils als Daumen, Zeige- und Mittelfinger der rechten Hand (Abb. 38 b). Wenn wir beide Teile der letzten Gleichheit auf dem rechten Skalar mit dem Vektor c multiplizieren, erhalten wir das Vektorprodukt der durch die Koordinaten gegebenen Vektoren. Gemischte Arbeit. Die Zahl rc c ist gleich der Höhe h des konstruierten Parallelepipeds, genommen mit dem „+“-Zeichen, wenn der Winkel zwischen den Vektoren c und c spitz ist (das Tripel a, b, c ist rechts), und mit dem Zeichen „ -” wenn der Winkel stumpf ist (das Tripel a, b, c - links), so dass also das gemischte Produkt der Vektoren a, b und c gleich dem Volumen V des Parallelepipeds ist, das auf diesen Vektoren wie auf Kanten aufgebaut ist wenn das Tripel a, b, c rechts ist, und -V, wenn das Tripel a , b, c - links ist. Basierend auf der geometrischen Bedeutung des gemischten Produkts können wir schlussfolgern, dass wir durch Multiplizieren derselben Vektoren a, b und c in beliebiger anderer Reihenfolge immer entweder +7 oder -K erhalten. Das Zeichen der pro-Abb. 38 Referenz hängt nur davon ab, welches Triplett die multiplizierten Vektoren bilden - rechts oder links. Wenn die Vektoren a, b, c ein rechtes Tripel bilden, dann sind auch die Tripel b, c, a und c, a, b recht. Gleichzeitig werden alle drei Tripel b, a, c; a, c, b und c, b, a - links. Also (a, b, c) = (b, c, a) = (c, a, b) = - (b, a, c) = - (a, c, b) = - (c, b , a). Wir betonen noch einmal, dass das Mischprodukt von Vektoren genau dann gleich Null ist, wenn die multiplizierten Vektoren a, b, c koplanar sind: (a, b, c sind koplanar) 7.2. Gemischtes Produkt in Koordinaten Die Vektoren a, b, c seien durch ihre Koordinaten in der Basis i, j, k gegeben: a = (x\,y\,z]), b= (x2,y2>z2), c = (x3, uz, 23). Finden wir einen Ausdruck für ihr Mischprodukt (a, b, c). Wir haben ein gemischtes Produkt von Vektoren, gegeben durch ihre Koordinaten in der Basis i, J, k, gleich der Determinante dritter Ordnung, deren Linien jeweils aus den Koordinaten der ersten, zweiten und dritten der multiplizierten zusammengesetzt sind Vektoren. Die notwendige und hinreichende Bedingung für die Komplanarität der Vektoren a y\, Z|), b = (xj Y2.22), c = (x3, uz, 23) kann in folgender Form geschrieben werden z, ar2 y2 -2 = 0. Uz-Beispiel. Prüfen Sie, ob die Vektoren v = (7,4,6), b = (2, 1,1), c = (19, II, 17) koplanar sind. Die betrachteten Vektoren sind koplanar oder nicht koplanar, je nachdem, ob die Determinante gleich Null ist oder nicht. Wenn wir sie in Bezug auf die Elemente der ersten Zeile erweitern, erhalten wir 7.3. Doppelkreuzprodukt Das Doppelkreuzprodukt [a, [b, c]] ist ein Vektor senkrecht zu den Vektoren a und [b, c]. Sie liegt daher in der Ebene der Vektoren b und c und kann in diese Vektoren expandiert werden. Es kann gezeigt werden, dass die Formel [a, [!>, c]] = b(a, e) - c(a, b) gilt. Aufgaben 1. Drei Vektoren AB = c, W? = o und CA = b dienen als Seiten des Dreiecks. Drücken Sie durch a, b und c die Vektoren aus, die mit den Medianen AM, DN, CP des Dreiecks zusammenfallen. 2. Welche Bedingung muss zwischen den Vektoren p und q bestehen, damit der Vektor p + q den Winkel zwischen ihnen halbiert? Es wird angenommen, dass alle drei Vektoren auf einen gemeinsamen Ursprung bezogen sind. 3. Berechnen Sie die Länge der Diagonalen des Parallelogramms, das auf den Vektoren a = 5p + 2q und b = p - 3q aufgebaut ist, wenn bekannt ist, dass |p| = 2v/2, |q| = 3 H-(p7ci) = f. 4. Bezeichnen Sie mit a und b die Seiten der Raute, die von einem gemeinsamen Scheitelpunkt ausgehen, und beweisen Sie, dass die Diagonalen der Raute senkrecht aufeinander stehen. 5. Berechnen Sie das Skalarprodukt der Vektoren a = 4i + 7j + 3k und b = 31 - 5j + k. 6. Finde den Einheitsvektor a0 parallel zum Vektor a = (6, 7, -6). 7. Finden Sie die Projektion des Vektors a = l+ j- kHa Vektor b = 21 - j - 3k. 8. Finden Sie den Kosinus des Winkels zwischen den Vektoren IS "w, wenn A (-4.0.4), B (-1.6.7), C (1.10.9). 9. Finden Sie einen Einheitsvektor p°, der gleichzeitig senkrecht auf dem Vektor a = (3, 6, 8) und der x-Achse steht. 10. Berechnen Sie den Sinus des Winkels zwischen den Diagonalen des Parallelophams, der auf den Vektoren a = 2i+J-k, b=i-3j + k wie auf den Seiten aufgebaut ist. Berechnen Sie die Höhe h des auf den Vektoren a = 31 + 2j - 5k, b = i-j + 4knc = i-3j + k aufgebauten Parallelepipeds, wenn das auf den Vektoren a und I aufgebaute Parallelogramm als Basis genommen wird). Antworten

Bevor wir uns dem Konzept eines Vektorprodukts zuwenden, wenden wir uns der Frage nach der Orientierung des geordneten Vektortripels a → , b → , c → im dreidimensionalen Raum zu.

Lassen Sie uns zunächst die Vektoren a → , b → , c → von einem Punkt beiseite legen. Die Orientierung des Tripels a → , b → , c → ist rechts oder links, je nach Richtung des Vektors c → . Aus der Richtung, in der die kürzeste Abbiegung vom Vektor a → nach b → vom Ende des Vektors c → erfolgt, wird die Form des Tripels a → , b → , c → bestimmt.

Wenn die kürzeste Drehung gegen den Uhrzeigersinn ist, wird das Tripel der Vektoren a → , b → , c → aufgerufen Rechts wenn im Uhrzeigersinn - links.

Als nächstes nehmen Sie zwei Kollineare Vektoren a → und b → . Verschieben wir dann die Vektoren A B → = a → und A C → = b → vom Punkt A. Konstruieren wir einen Vektor A D → = c → , der gleichzeitig senkrecht auf A B → und A C → steht. Wenn wir also den Vektor A D → = c → konstruieren, können wir zwei Dinge tun, indem wir ihm entweder eine Richtung oder die entgegengesetzte geben (siehe Abbildung).

Das geordnete Trio der Vektoren a → , b → , c → kann, wie wir herausgefunden haben, je nach Richtung des Vektors rechts oder links sein.

Aus dem Obigen können wir die Definition eines Vektorprodukts einführen. Diese Definition wird für zwei Vektoren gegeben, die in einem rechteckigen Koordinatensystem des dreidimensionalen Raums definiert sind.

Bestimmung 1

Das Vektorprodukt zweier Vektoren a → und b → Wir nennen einen solchen Vektor, der in einem rechteckigen Koordinatensystem des dreidimensionalen Raums gegeben ist, so dass:

• wenn die Vektoren a → und b → kollinear sind, ist es Null;
• es wird sowohl zum Vektor a →​​ als auch zum Vektor b → senkrecht sein, d.h. ∠ a → c → = ∠ b → c → = π 2 ;
• seine Länge wird durch die Formel bestimmt: c → = a → b → sin ∠ a → , b → ;
• das Tripel der Vektoren a → , b → , c → hat die gleiche Orientierung wie das gegebene Koordinatensystem.

Das Kreuzprodukt der Vektoren a → und b → hat die folgende Notation: a → × b → .

Produktübergreifende Koordinaten

Da jeder Vektor bestimmte Koordinaten im Koordinatensystem hat, ist es möglich, eine zweite Definition des Kreuzprodukts einzuführen, die es Ihnen ermöglicht, seine Koordinaten aus den gegebenen Koordinaten der Vektoren zu finden.

Bestimmung 2

In einem rechtwinkligen Koordinatensystem des dreidimensionalen Raums Vektorprodukt zweier Vektoren a → = (a x ; a y ; a z) und b → = (b x ; b y ; b z) nenne den Vektor c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , wobei i → , j → , k → Koordinatenvektoren sind.

Das Vektorprodukt kann als Determinante einer quadratischen Matrix dritter Ordnung dargestellt werden, wobei die erste Zeile die ora-Vektoren i → , j → , k → enthält, die zweite Zeile die Koordinaten des Vektors a → enthält und die dritte die Koordinaten des Vektors b → in einem gegebenen rechtwinkligen Koordinatensystem sind, sieht diese Matrixdeterminante so aus: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Wenn wir diese Determinante über die Elemente der ersten Zeile erweitern, erhalten wir die Gleichheit: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b y k → = = a → × b → = ( a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Produktübergreifende Eigenschaften

Es ist bekannt, dass das Vektorprodukt in Koordinaten als Determinante der Matrix dargestellt wird c → = a → × b → = i → j → k → a x a y a z b x b y b z , dann auf der Basis matrixbestimmende Eigenschaften folgende Vektorprodukteigenschaften:

1. Antikommutativität a → × b → = - b → × a → ;
2. Distributivität a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → oder a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. Assoziativität λ a → × b → = λ a → × b → oder a → × (λ b →) = λ a → × b → , wobei λ eine beliebige reelle Zahl ist.

Diese Eigenschaften haben keine komplizierten Beweise.

Beispielsweise können wir die Antikommutativitätseigenschaft eines Vektorprodukts beweisen.

Beweis der Antikommutativität

Per Definition ist a → × b → = i → j → k → a x a y a z b x b y b z und b → × a → = i → j → k → b x b y b z a x a y a z . Und wenn zwei Zeilen der Matrix vertauscht sind, sollte sich der Wert der Determinante der Matrix ins Gegenteil ändern, also a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , was die Antikommutativität des Vektorprodukts beweist.

Vektorprodukt - Beispiele und Lösungen

In den meisten Fällen gibt es drei Arten von Aufgaben.

Bei Problemen des ersten Typs sind normalerweise die Längen zweier Vektoren und der Winkel zwischen ihnen angegeben, aber Sie müssen die Länge des Kreuzprodukts finden. Verwenden Sie in diesem Fall die folgende Formel c → = a → b → sin ∠ a → , b → .

Beispiel 1

Finden Sie die Länge des Kreuzprodukts der Vektoren a → und b → wenn a → = 3 , b → = 5 , ∠ a → , b → = π 4 bekannt ist.

Lösung

Mit der Definition der Länge des Vektorprodukts der Vektoren a → und b → lösen wir dieses Problem: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Antworten: 15 2 2 .

Aufgaben des zweiten Typs haben einen Zusammenhang mit den Koordinaten von Vektoren, sie enthalten ein Vektorprodukt, seine Länge usw. bekannte Koordinaten durchsucht gegebene Vektoren a → = (a x ; a y ; a z) und b → = (b x ; b y ; b z) .

Für diese Art von Aufgabe können Sie viele Optionen für Aufgaben lösen. Beispielsweise nicht die Koordinaten der Vektoren a → und b → , sondern deren Erweiterungen in Koordinatenvektoren der Form b → = b x ich → + b y j → + b z k → und c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , oder die Vektoren a → und b → können durch die Koordinaten ihrer gegeben werden Start- und Endpunkte.

Betrachten Sie die folgenden Beispiele.

Beispiel 2

Zwei Vektoren werden in einem rechtwinkligen Koordinatensystem a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) gesetzt. Finden Sie ihr Vektorprodukt.

Lösung

Durch die zweite Definition finden wir das Vektorprodukt zweier Vektoren in angegebenen Koordinaten: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + (( - 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 ich → - 2 j → - 2 k → .

Wenn wir das Vektorprodukt durch die Matrixdeterminante schreiben, dann lautet die Lösung dieses Beispiels wie folgt: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 ich → - 2 j → - 2 k → .

Antworten: a → × b → = - 2 ich → - 2 j → - 2 k → .

Beispiel 3

Finden Sie die Länge des Kreuzprodukts der Vektoren i → - j → und i → + j → + k → , wobei i → , j → , k → - Orte eines rechtwinkligen kartesischen Koordinatensystems.

Lösung

Lassen Sie uns zuerst die Koordinaten des gegebenen Vektorprodukts i → - j → × i → + j → + k → im gegebenen rechtwinkligen Koordinatensystem finden.

Es ist bekannt, dass die Vektoren i → – j → und i → + j → + k → die Koordinaten (1 ; – 1 ; 0) bzw. (1 ; 1 ; 1) haben. Finden Sie die Länge des Vektorprodukts mit der Matrixdeterminante, dann haben wir i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2k → .

Daher hat das Vektorprodukt i → - j → × i → + j → + k → Koordinaten (- 1 ; - 1 ; 2) im gegebenen Koordinatensystem.

Wir finden die Länge des Vektorprodukts durch die Formel (siehe Abschnitt zum Ermitteln der Länge des Vektors): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Antworten: ich → - j → × ich → + j → + k → = 6 . .

Beispiel 4

Die Koordinaten von drei Punkten A (1 , 0 , 1) , B (0 , 2 , 3) ​​​​, C (1 , 4 , 2) werden in einem rechteckigen kartesischen Koordinatensystem angegeben. Finden Sie gleichzeitig einen Vektor, der senkrecht zu A B → und A C → steht.

Lösung

Die Vektoren A B → und A C → haben die folgenden Koordinaten (- 1 ; 2 ; 2) bzw. (0 ; 4 ; 1). Nachdem wir das Vektorprodukt der Vektoren A B → und A C → gefunden haben, ist es offensichtlich, dass es per Definition ein senkrechter Vektor sowohl zu A B → als auch zu A C → ist, das heißt, es ist die Lösung unseres Problems. Finde es A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Antworten: - 6 ich → + j → - 4 k → . ist einer der senkrechten Vektoren.

Probleme des dritten Typs konzentrieren sich auf die Verwendung der Eigenschaften des Vektorprodukts von Vektoren. Nach deren Anwendung erhalten wir eine Lösung für das gegebene Problem.

Beispiel 5

Die Vektoren a → und b → sind senkrecht und haben die Längen 3 bzw. 4. Finden Sie die Länge des Kreuzprodukts 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Lösung

Durch die Verteilungseigenschaft des Vektorprodukts können wir schreiben 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Durch die Eigenschaft der Assoziativität nehmen wir im letzten Ausdruck die numerischen Koeffizienten jenseits des Vorzeichens von Vektorprodukten heraus: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Die Vektorprodukte a → × a → und b → × b → sind gleich 0, da a → × a → = a → a → sin 0 = 0 und b → × b → = b → b → sin 0 = 0 , dann 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

Aus der Antikommutativität des Vektorprodukts folgt - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Unter Verwendung der Eigenschaften des Vektorprodukts erhalten wir die Gleichheit 3 ​​· a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Bedingt sind die Vektoren a → und b → senkrecht zueinander, das heißt, der Winkel zwischen ihnen ist gleich π 2 . Jetzt müssen nur noch die gefundenen Werte in die entsprechenden Formeln eingesetzt werden: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Antworten: 3 a → - b → × a → - 2 b → = 60 .

Die Länge des Kreuzprodukts von Vektoren ist per Definition a → × b → = a → · b → · sin ∠ a → , b → . Da bereits (aus dem Schulkurs) bekannt ist, dass die Fläche eines Dreiecks gleich dem halben Produkt der Längen seiner beiden Seiten multipliziert mit dem Sinus des Winkels zwischen diesen Seiten ist. Daher ist die Länge des Vektorprodukts gleich der Fläche eines Parallelogramms - eines doppelten Dreiecks, nämlich des Produkts der Seiten in Form der Vektoren a → und b → , die von einem Punkt durch den Sinus abgesetzt werden des Winkels zwischen ihnen sin ∠ a → , b → .

Dies ist die geometrische Bedeutung des Vektorprodukts.

Die physikalische Bedeutung des Vektorprodukts

In der Mechanik, einem Teilgebiet der Physik, kann man dank des Vektorprodukts das Kraftmoment relativ zu einem Punkt im Raum bestimmen.

Bestimmung 3

Unter dem Moment der Kraft F → , angewendet auf Punkt B, relativ zu Punkt A, verstehen wir das folgende Vektorprodukt A B → × F → .

Wenn Sie einen Fehler im Text bemerken, markieren Sie ihn bitte und drücken Sie Strg+Enter

Eigenschaften des Punktprodukts

Skalarprodukt Vektoren, Definition, Eigenschaften

Lineare Operationen auf Vektoren.

Vektoren, grundlegende Konzepte, Definitionen, lineare Operationen an ihnen

Ein Vektor auf einer Ebene ist ein geordnetes Paar seiner Punkte, wobei der erste Punkt der Anfang und der zweite das Ende des Vektors genannt wird

Zwei Vektoren heißen gleich, wenn sie gleich und gleichgerichtet sind.

Vektoren, die auf derselben Linie liegen, werden als kodirektional bezeichnet, wenn sie mit einem Teil desselben Vektors kodirektional sind, der nicht auf dieser Linie liegt.

Vektoren, die auf derselben Linie oder auf parallelen Linien liegen, werden kollinear genannt, und kollinear, aber nicht kodirektional, werden als entgegengesetzt gerichtet bezeichnet.

Vektoren, die auf senkrechten Linien liegen, heißen orthogonal.

Definition 5.4. Summe a+b Vektoren a und b heißt der Vektor, der vom Anfang des Vektors kommt a bis zum Ende des Vektors b , wenn der Anfang des Vektors b fällt mit dem Ende des Vektors zusammen a .

Definition 5.5. Unterschied a - b Vektoren a und b ein solcher Vektor heißt Mit , die zusammen mit dem Vektor b ergibt einen Vektor a .

Definition 5.6. Arbeitk a Vektor a pro Zahl k Vektor genannt b , Kollinearer Vektor a , dessen Modul gleich | ist k||a | und eine Richtung, die mit der Richtung identisch ist a bei k>0 und umgekehrt a bei k<0.

Eigenschaften der Multiplikation eines Vektors mit einer Zahl:

Eigentum 1. k(a+b ) = k a+ k b.

Eigenschaft 2. (k+m)a = k a+ m a.

Eigenschaft 3. k(m a) = (km)a .

Folge. Wenn Nicht-Null-Vektoren a und b kollinear sind, dann gibt es eine Zahl k, was b= k a.

Das Skalarprodukt zweier Vektoren ungleich Null a und b eine Zahl (skalar) genannt, die gleich dem Produkt der Längen dieser Vektoren und dem Kosinus des Winkels φ zwischen ihnen ist. Das Skalarprodukt kann auf verschiedene Weise ausgedrückt werden, zum Beispiel als ab, a · b, (a , b), (a · b). Das Skalarprodukt ist also:

a · b = |a| · | b| cos φ

Wenn mindestens einer der Vektoren gleich Null ist, dann ist das Skalarprodukt gleich Null.

Permutationseigenschaft: a · b = b · a(das Skalarprodukt ändert sich nicht durch Permutation von Faktoren);

Verteilungseigenschaft: a · ( b · c) = (a · b) · c(das Ergebnis hängt nicht von der Reihenfolge der Multiplikation ab);

Kombinationseigenschaft (bezogen auf den Skalarfaktor): (λ a) · b = λ ( a · b).

Eigenschaft der Orthogonalität (Rechtwinkligkeit): wenn der Vektor a und b nicht Null, dann ist ihr Skalarprodukt nur dann Null, wenn diese Vektoren orthogonal (senkrecht zueinander) sind. a ┴ b;

Quadratisches Eigentum: a · a = a 2 = |a| 2 (das Skalarprodukt eines Vektors mit sich selbst ist gleich dem Quadrat seines Betrags);

Wenn die Koordinaten der Vektoren a= (x 1 , y 1 , z 1 ) und b=(x 2 , y 2 , z 2 ), dann ist das Skalarprodukt a · b= x 1 x 2 + y 1 y 2 + z 1 z 2 .

Vektor, der Vektoren hält. Definition: Das Vektorprodukt zweier Vektoren und wird als Vektor verstanden, für den gilt:

Das Modul ist gleich der Fläche des auf diesen Vektoren aufgebauten Parallelogramms, d.h. , wobei der Winkel zwischen den Vektoren und ist

Dieser Vektor steht senkrecht auf den multiplizierten Vektoren, d.h.

Wenn die Vektoren nicht kollinear sind, dann bilden sie ein rechtes Tripel von Vektoren.

Produktübergreifende Eigenschaften:

1. Wenn die Reihenfolge der Faktoren geändert wird, ändert das Vektorprodukt sein Vorzeichen in das entgegengesetzte, wobei der Modul erhalten bleibt, d.h.

2 .Vektorquadrat ist gleich Nullvektor, d.h.

3 .Der Skalarfaktor kann aus dem Vorzeichen des Vektorprodukts genommen werden, d.h.

4 .Für drei beliebige Vektoren die Gleichheit

5 .Notwendige und hinreichende Bedingung für die Kollinearität zweier Vektoren und :