Vektorprodukt av vektorer. Blandad produkt av vektorer

Definition. Vektorprodukten av en vektor a (multiplikator) med en vektor (multiplikator) som inte är kolinjär med den är den tredje vektorn c (produkt), som är konstruerad enligt följande:

1) dess modul är numeriskt lika med arean av parallellogrammet i fig. 155), byggd på vektorer, d. v. s. den är lika med riktningen vinkelrät mot planet för nämnda parallellogram;

3) i detta fall väljs vektorns c riktning (av två möjliga) så att vektorerna c bildar ett högerhänt system (§ 110).

Beteckning: eller

Tillägg till definitionen. Om vektorerna är kolinjära, då betraktar figuren som ett (villkorligt) parallellogram, är det naturligt att tilldela noll area. Därför anses vektorprodukten av kolinjära vektorer vara lika med nollvektorn.

Eftersom nollvektorn kan tilldelas vilken riktning som helst, motsäger denna konvention inte punkterna 2 och 3 i definitionen.

Anmärkning 1. I termen "vektorprodukt" anger det första ordet att resultatet av en handling är en vektor (till skillnad från en skalär produkt; jfr 104 § anmärkning 1).

Exempel 1. Hitta vektorprodukten där huvudvektorerna för det högra koordinatsystemet (Fig. 156).

1. Eftersom längderna på huvudvektorerna är lika med skalenheten, är arean av parallellogrammet (kvadrat) numeriskt lika med en. Därför är modulen för vektorprodukten lika med ett.

2. Eftersom vinkelrät mot planet är axeln, är den önskade vektorprodukten en vektor kolinjär med vektorn k; och eftersom båda har modul 1 är den erforderliga korsprodukten antingen k eller -k.

3. Av dessa två möjliga vektorer måste den första väljas, eftersom vektorerna k bildar ett höger system (och vektorerna bildar ett vänster).

Exempel 2. Hitta korsprodukten

Lösning. Som i exempel 1 drar vi slutsatsen att vektorn är antingen k eller -k. Men nu måste vi välja -k, eftersom vektorerna bildar det högra systemet (och vektorerna bildar det vänstra). Så,

Exempel 3 Vektorerna har längder på 80 respektive 50 cm och bildar en vinkel på 30°. Ta en meter som en längdenhet och hitta längden på vektorprodukten a

Lösning. Arean av ett parallellogram byggt på vektorer är lika med Längden på den önskade vektorprodukten är lika med

Exempel 4. Hitta längden på korsprodukten av samma vektorer, ta en centimeter som en längdenhet.

Lösning. Eftersom arean av parallellogrammet byggt på vektorer är lika med längden på vektorprodukten är 2000 cm, dvs.

Jämförelse av exempel 3 och 4 visar att vektorns längd inte bara beror på faktorernas längder utan också på valet av längdenhet.

Den fysiska betydelsen av vektorprodukten. Av de många fysiska storheter som representeras av vektorprodukten kommer vi bara att betrakta kraftmomentet.

Låt A vara kraftens appliceringspunkt. Kraftmomentet i förhållande till punkten O kallas vektorprodukten. Eftersom modulen för denna vektorprodukt är numeriskt lika med parallellogrammets area (fig. 157), momentets modul är lika med produkten av basen med höjden, d.v.s. kraften multiplicerad med avståndet från punkten O till den räta linjen längs vilken kraften verkar.

Inom mekaniken är det bevisat att för jämvikten hos en stel kropp är det nödvändigt att inte bara summan av vektorerna som representerar krafterna som appliceras på kroppen, utan också summan av kraftmomenten ska vara lika med noll. I det fall då alla krafter är parallella med samma plan, kan additionen av vektorerna som representerar momenten ersättas med addition och subtraktion av deras moduler. Men för godtyckliga kraftriktningar är en sådan ersättning omöjlig. I enlighet med detta definieras korsprodukten exakt som en vektor och inte som ett tal.

BLANDAD PRODUKT AV TRE VEKTORER OCH DESS EGENSKAPER

blandad produkt tre vektorer kallas ett tal lika med . Betecknas . Här multipliceras de två första vektorerna vektoriellt och sedan multipliceras den resulterande vektorn skalärt med den tredje vektorn. Uppenbarligen är en sådan produkt något nummer.

Tänk på egenskaperna hos den blandade produkten.

1. geometrisk känsla blandad produkt. blandad produkt 3 vektorer, upp till ett tecken, är lika med volymen av parallellepipeden byggd på dessa vektorer, som på kanter, d.v.s. .

   Alltså och .

   

   Bevis. Låt oss skjuta upp vektorerna från det gemensamma ursprunget och bygga en parallellepiped på dem. Låt oss beteckna och notera det. Per definition punkt produkt

   Förutsatt att och betecknar igenom h höjden på parallellepipeden finner vi .

   Alltså kl

   Om , då och . Följaktligen.

   Genom att kombinera båda dessa fall får vi eller .

   Av beviset för denna egenskap, i synnerhet, följer att om trippeln av vektorer är rätt, då den blandade produkten , och om den är vänster, då .

2. För alla vektorer , , jämlikheten

   Beviset för denna egenskap följer av egenskap 1. Det är faktiskt lätt att visa att och . Dessutom tas tecknen "+" och "-" samtidigt, eftersom vinklarna mellan vektorerna och och och är både spetsiga eller trubbiga.

3. När två olika faktorer byts om byter den blandade produkten tecken.

   Faktum är att om vi betraktar den blandade produkten , då, till exempel, eller

4. En blandad produkt om och endast om en av faktorerna är lika med noll eller om vektorerna är koplanära.

   Bevis.

   Således är ett nödvändigt och tillräckligt villkor för komplanariteten hos 3 vektorer lika med noll av deras blandade produkt. Dessutom följer av detta att tre vektorer utgör en bas i rymden om .

   Om vektorerna ges i koordinatform, kan det visas att deras blandade produkt hittas med formeln:

   .

   Således är den blandade produkten lika med en tredje ordningens determinant vars första linje innehåller koordinaterna för den första vektorn, den andra raden innehåller koordinaterna för den andra vektorn och den tredje raden innehåller koordinaterna för den tredje vektorn.

   Exempel.

ANALYTISK GEOMETRI I RYMMEN

Ekvationen F(x, y, z)= 0 definierar i rymden Oxyz någon yta, dvs. plats för punkter vars koordinater x, y, z uppfylla denna ekvation. Denna ekvation kallas ytekvationen, och x, y, z– aktuella koordinater.

Men ofta definieras ytan inte av en ekvation, utan som en uppsättning punkter i rymden som har en eller annan egenskap. I det här fallet krävs det att hitta ytans ekvation, baserat på dess geometriska egenskaper.

PLAN.

NORMAL PLAN VEKTOR.

EKVATION FÖR ETT PLAN SOM GÅR GENOM EN GIVET PUNKT

Betrakta ett godtyckligt plan σ i rymden. Dess position bestäms genom att sätta en vektor vinkelrätt mot detta plan, och någon fast punkt M0(x0, y 0, z0) liggande i planet σ.

Vektorn vinkelrät mot planet σ kallas vanligt vektor för detta plan. Låt vektorn ha koordinater.

Vi härleder ekvationen för planet σ som går genom den givna punkten M0 och har en normal vektor. För att göra detta, ta en godtycklig punkt på planet σ M(x, y, z) och överväga vektorn.

För vilken punkt som helst MÎ σ vektor. Därför är deras skalära produkt lika med noll. Denna jämlikhet är villkoret att poängen MО σ. Den är giltig för alla punkter på detta plan och bryts så snart som punkten M kommer att vara utanför planet σ.

Om vi ​​betecknar punkterna med radievektorn M, är radievektorn för punkten M0, då kan ekvationen skrivas som

Denna ekvation kallas vektor plan ekvation. Låt oss skriva det i koordinatform. Sedan dess

Så vi har fått ekvationen för planet som passerar genom den givna punkten. För att komponera ekvationen för planet måste du alltså känna till koordinaterna för normalvektorn och koordinaterna för någon punkt som ligger på planet.

Observera att ekvationen för planet är en ekvation av 1:a graden med avseende på de aktuella koordinaterna x, y och z.

Exempel.

ALLMÄN EKVATION FÖR PLANET

Det kan visas att varje ekvation av första graden med avseende på kartesiska koordinater x, y, zär en ekvation för något plan. Denna ekvation skrivs som:

Axe+By+Cz+D=0

och ringde allmän ekvation planet och koordinaterna A, B, C här är koordinaterna för planets normalvektor.

Låt oss överväga särskilda fall av den allmänna ekvationen. Låt oss ta reda på hur planet ligger i förhållande till koordinatsystemet om en eller flera koefficienter i ekvationen försvinner.

A är längden på segmentet avskuret av planet på axeln Oxe. På samma sätt kan man visa det b och cär längderna på segmenten avskurna av det betraktade planet på axlarna Oj och Uns.

Det är bekvämt att använda ekvationen för ett plan i segment för att konstruera plan.

Denna online-kalkylator beräknar korsprodukten av vektorer. En detaljerad lösning ges. För att beräkna korsprodukten av vektorer, skriv in koordinaterna för vektorerna i cellerna och klicka på "Beräkna".

×

Varning

Rensa alla celler?

Stäng Rensa

Datainmatningsinstruktion. Tal anges som heltal (exempel: 487, 5, -7623, etc.), decimaltal (t.ex. 67., 102.54, etc.) eller bråktal. Bråket måste skrivas i formen a/b, där a och b (b>0) är heltal eller decimaltal. Exempel 45/5, 6,6/76,4, -7/6,7 osv.

Korsprodukt av vektorer

Innan du går vidare till definitionen av vektorprodukten av vektorer, överväg begreppen ordnad trippel av vektorer, vänster trippel av vektorer, höger trippel av vektorer.

Definition 1. Tre vektorer kallas beställde trippel(eller trippel) om det anges vilken av dessa vektorer som är den första, vilken är den andra och vilken som är den tredje.

Inspelning cba- betyder - den första är en vektor c, den andra är vektorn b och den tredje är vektorn a.

Definition 2. En trippel av icke-samplanära vektorer abc kallas höger (vänster) om, när de reduceras till en gemensam början, dessa vektorer är ordnade som de stora, oböjda pek- och långfingrarna på höger (vänster) hand är placerade.

Definition 2 kan formuleras på annat sätt.

Definition 2. En trippel av icke-samplanära vektorer abc kallas höger (vänster) om, när den reduceras till ett gemensamt ursprung, vektorn c placerad på andra sidan av planet som definieras av vektorerna a och b, varifrån den kortaste svängen a till b utförs moturs (medurs).

Vektor trio abc visad i fig. 1 är rätt och trippel abc visad i fig. 2 är kvar.

Om två trippel av vektorer är höger eller vänster, sägs de ha samma orientering. Annars sägs de vara av motsatt orientering.

Definition 3. Ett kartesiskt eller affint koordinatsystem kallas höger (vänster) om de tre basvektorerna bildar en höger (vänster) trippel.

För tydlighetens skull kommer vi i det följande endast att överväga högerhänta koordinatsystem.

Definition 4. vektor konst vektor a per vektor b kallas vektor Med, betecknad med symbolen c=[ab] (eller c=[a,b], eller c=a×b) och uppfyller följande tre krav:

• vektor längd Medär lika med produkten av vektorernas längder a och b till vinkelns sinus φ mellan dem:

|c|=|[ab]|=|a||b|sinφ;

(1)

• vektor Med ortogonal mot var och en av vektorerna a och b;
• vektor c riktade så att de tre abcär rätt.

Korsprodukten av vektorer har följande egenskaper:

• [ab]=−[ba] (antipermutabilitet faktorer);
• [(λa)b]=λ [ab] (kompatibilitet i förhållande till den numeriska faktorn);
• [(a+b)c]=[ac]+[bc] (distribution relativt summan av vektorer);
• [aa]=0 för vilken vektor som helst a.

Geometriska egenskaper för korsprodukten av vektorer

Sats 1. För att två vektorer ska vara kolinjära är det nödvändigt och tillräckligt att deras vektorprodukt är lika med noll.

Bevis. Behöver. Låt vektorerna a och b kolinjär. Då är vinkeln mellan dem 0 eller 180° och sinφ=synd180=synd 0=0. Därför, med hänsyn till uttryck (1), längden på vektorn cär lika med noll. Sedan c noll vektor.

Lämplighet. Låt korsprodukten av vektorer a och b nav till noll: [ ab]=0. Låt oss bevisa att vektorerna a och b kolinjär. Om minst en av vektorerna a och b noll, då är dessa vektorer kolinjära (eftersom nollvektorn har en obestämd riktning och kan betraktas som kolinjär med vilken vektor som helst).

Om båda vektorerna a och b icke noll, sedan | a|>0, |b|>0. Sedan från [ ab]=0 och av (1) följer det sinφ=0. Därav vektorerna a och b kolinjär.

Teoremet har bevisats.

Sats 2. Längden (modulen) av vektorprodukten [ ab] är lika med arean S parallellogram byggt på vektorer reducerade till ett gemensamt ursprung a och b.

Bevis. Som du vet är arean av ett parallellogram lika med produkten av de intilliggande sidorna av detta parallellogram och sinus för vinkeln mellan dem. Följaktligen:

Då har korsprodukten av dessa vektorer formen:

Om vi ​​expanderar determinanten över elementen i den första raden får vi uppdelningen av vektorn a×b grund i, j, k, vilket är ekvivalent med formel (3).

Bevis för sats 3. Komponera alla möjliga par av basvektorer i, j, k och beräkna deras vektorprodukt. Man bör ta hänsyn till att basvektorerna är ömsesidigt ortogonala, bildar en rät trippel och har enhetslängd (med andra ord kan vi anta att i={1, 0, 0}, j={0, 1, 0}, k=(0, 0, 1)). Då har vi:

Från den senaste jämlikhet och relationer (4) får vi:

Komponera en 3×3-matris, vars första rad är basvektorerna jag, j, k, och de återstående raderna är fyllda med element av vektorer a och b.

Innan vi ger begreppet en vektorprodukt, låt oss vända oss till frågan om orienteringen av den ordnade trippeln av vektorer a → , b → , c → i tredimensionellt rymd.

Till att börja med, låt oss lägga åt sidan vektorerna a → , b → , c → från en punkt. Orienteringen av trippeln a → , b → , c → är höger eller vänster, beroende på vektorns c → riktning. Från den riktning i vilken den kortaste svängen görs från vektorn a → till b → från slutet av vektorn c → , kommer formen av trippeln a → , b → , c → att bestämmas.

Om den kortaste rotationen är moturs, kallas trippeln av vektorer a → , b → , c → höger om medurs - vänster.

Ta sedan två icke-kollinjära vektorer a → och b → . Låt oss sedan skjuta upp vektorerna A B → = a → och A C → = b → från punkten A. Låt oss konstruera en vektor A D → = c → , som samtidigt är vinkelrät mot både A B → och A C → . När vi konstruerar vektorn A D → = c → kan vi alltså göra två saker, ge den antingen en riktning eller motsatt (se illustrationen).

Den ordnade trion av vektorer a → , b → , c → kan, som vi fick reda på, vara höger eller vänster beroende på vektorns riktning.

Från ovanstående kan vi introducera definitionen av en vektorprodukt. Denna definition ges för två vektorer definierade i ett rektangulärt koordinatsystem av tredimensionellt rymd.

Definition 1

Vektorprodukten av två vektorer a → och b → vi kallar en sådan vektor given i ett rektangulärt koordinatsystem av tredimensionellt rymd så att:

• om vektorerna a → och b → är kolinjära kommer den att vara noll;
• den kommer att vara vinkelrät mot både vektor a →​​ och vektor b → dvs. ∠ a → c → = ∠ b → c → = π 2 ;
• dess längd bestäms av formeln: c → = a → b → sin ∠ a → , b → ;
• tripletten av vektorerna a → , b → , c → har samma orientering som det givna koordinatsystemet.

Korsprodukten av vektorerna a → och b → har följande notation: a → × b → .

Korsa produktkoordinater

Eftersom vilken vektor som helst har vissa koordinater i koordinatsystemet, är det möjligt att införa en andra definition av vektorprodukten, som gör att du kan hitta dess koordinater från de givna koordinaterna för vektorerna.

Definition 2

I ett rektangulärt koordinatsystem av tredimensionellt rymd vektorprodukt av två vektorer a → = (a x ; a y ; a z) och b → = (b x ; b y ; b z) kalla vektorn c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , där i → , j → , k → är koordinatvektorer.

Vektorprodukten kan representeras som en determinant av en kvadratisk matris av tredje ordningen, där den första raden är orta-vektorerna i → , j → , k → , den andra raden innehåller koordinaterna för vektorn a → , och den tredje är koordinaterna för vektorn b → i ett givet rektangulärt koordinatsystem, ser denna matrisdeterminant ut så här: c → = a → × b → = i → j → k → a x a y a z b x b y b z

Om vi ​​expanderar denna determinant över elementen i den första raden får vi likheten: c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b → b → a k (→ x a y b → b → a k a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Kors produktegenskaper

Det är känt att vektorprodukten i koordinater representeras som determinanten för matrisen c → = a → × b → = i → j → k → a x a y a z b x b y b z , sedan på basen matrisdeterminantegenskaper det följande vektor produktegenskaper:

1. antikommutativitet a → × b → = - b → × a → ;
2. distributivitet a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → eller a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. associativitet λ a → × b → = λ a → × b → eller a → × (λ b →) = λ a → × b → , där λ är ett godtyckligt reellt tal.

Dessa egenskaper har inte komplicerade bevis.

Till exempel kan vi bevisa antikommutativiteten hos en vektorprodukt.

Bevis på antikommutativitet

Per definition, a → × b → = i → j → k → a x a y a z b x b y b z och b → × a → = i → j → k → b x b y b z a x a y a z. Och om två rader i matrisen byts om, bör värdet på matrisens determinant ändras till det motsatta, därför a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y a z = - b → × a → , vilket och bevisar antikommutativiteten hos vektorprodukten.

Vektorprodukt - exempel och lösningar

I de flesta fall finns det tre typer av uppgifter.

I problem av den första typen anges vanligtvis längden på två vektorer och vinkeln mellan dem, men du måste hitta längden på korsprodukten. Använd i det här fallet följande formel c → = a → b → sin ∠ a → , b → .

Exempel 1

Hitta längden på korsprodukten av vektorerna a → och b → om a → = 3 , b → = 5 , ∠ a → , b → = π 4 är känd.

Lösning

Med hjälp av definitionen av längden av vektorprodukten av vektorerna a → och b → löser vi detta problem: a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2 .

Svar: 15 2 2 .

Uppgifter av den andra typen har ett samband med vektorernas koordinater, de innehåller en vektorprodukt, dess längd etc. sökte genom kända koordinater givna vektorer a → = (a x ; a y ; a z) och b → = (b x ; b y ; b z) .

För den här typen av uppgifter kan du lösa många alternativ för uppgifter. Till exempel inte koordinaterna för vektorerna a → och b → , utan deras expansioner i formens koordinatvektorer b → = b x i → + b y j → + b z k → och c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , eller så kan vektorerna a → och b → ges av koordinaterna för deras start- och slutpunkter.

Betrakta följande exempel.

Exempel 2

Två vektorer sätts i ett rektangulärt koordinatsystem a → = (2 ; 1 ; - 3), b → = (0 ; - 1 ; 1) . Hitta deras vektorprodukt.

Lösning

Enligt den andra definitionen hittar vi vektorprodukten av två vektorer i givna koordinater: a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 k → .

Om vi ​​skriver vektorprodukten genom matrisdeterminanten, så är lösningen i detta exempel följande: a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 = - 2 i → - 2 j → - 2 k → .

Svar: a → × b → = - 2 i → - 2 j → - 2 k → .

Exempel 3

Hitta längden på korsprodukten av vektorerna i → - j → och i → + j → + k → , där i → , j → , k → - orter av ett rektangulärt kartesiskt koordinatsystem.

Lösning

Låt oss först hitta koordinaterna för den givna vektorprodukten i → - j → × i → + j → + k → i det givna rektangulära koordinatsystemet.

Det är känt att vektorerna i → - j → och i → + j → + k → har koordinater (1 ; - 1 ; 0) respektive (1 ; 1 ; 1). Hitta längden på vektorprodukten med hjälp av matrisdeterminanten, då har vi i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Därför har vektorprodukten i → - j → × i → + j → + k → koordinater (- 1 ; - 1 ; 2) i det givna koordinatsystemet.

Vi hittar längden på vektorprodukten med formeln (se avsnittet om att hitta vektorns längd): i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Svar: i → - j → x i → + j → + k → = 6 . .

Exempel 4

Koordinaterna för tre punkter A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) ges i ett rektangulärt kartesiskt koordinatsystem. Hitta någon vektor vinkelrät mot A B → och A C → samtidigt.

Lösning

Vektorerna A B → och A C → har följande koordinater (-1 ; 2 ; 2) respektive (0 ; 4 ; 1). Efter att ha hittat vektorprodukten av vektorerna A B → och A C → , är det uppenbart att det är en vinkelrät vektor per definition till både A B → och A C → , det vill säga att det är lösningen på vårt problem. Hitta det A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k → .

Svar: - 6 i → + j → - 4 k → . är en av de vinkelräta vektorerna.

Problem av den tredje typen är fokuserade på att använda egenskaperna hos vektorprodukten av vektorer. Efter att ha ansökt vilken, kommer vi att få en lösning på det givna problemet.

Exempel 5

Vektorerna a → och b → är vinkelräta och deras längder är 3 respektive 4. Hitta längden på korsprodukten 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → .

Lösning

Med fördelningsegenskapen för vektorprodukten kan vi skriva 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Genom egenskapen associativitet tar vi ut de numeriska koefficienterna bortom tecknet för vektorprodukter i det sista uttrycket: 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

Vektorprodukterna a → × a → och b → × b → är lika med 0, eftersom a → × a → = a → a → sin 0 = 0 och b → × b → = b → b → sin 0 = 0 , sedan 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

Av vektorproduktens antikommutativitet följer - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Med hjälp av vektorproduktens egenskaper får vi likheten 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → .

Av villkor är vektorerna a → och b → vinkelräta, det vill säga vinkeln mellan dem är lika med π 2 . Nu återstår bara att ersätta de hittade värdena i motsvarande formler: 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60.

Svar: 3a → - b → x a → - 2 b → = 60 .

Längden på vektorernas korsprodukt är per definition a → × b → = a → · b → · sin ∠ a → , b → . Eftersom det redan är känt (från skolkursen) att arean av en triangel är lika med hälften av produkten av längderna på dess två sidor multiplicerat med sinus för vinkeln mellan dessa sidor. Därför är längden på vektorprodukten lika med arean av ett parallellogram - en fördubblad triangel, nämligen produkten av sidorna i form av vektorerna a → och b → , avskild från en punkt, med sinus av vinkeln mellan dem sin ∠ a → , b → .

Detta är den geometriska betydelsen av vektorprodukten.

Den fysiska betydelsen av vektorprodukten

Inom mekaniken, en av fysikens grenar, kan du tack vare vektorprodukten bestämma kraftmomentet i förhållande till en punkt i rymden.

Definition 3

Under kraftmomentet F → , applicerad på punkt B , relativt punkt A kommer vi att förstå följande vektorprodukt A B → × F → .

Om du märker ett fel i texten, markera det och tryck på Ctrl+Enter

Uppenbarligen, i fallet med en korsprodukt, spelar ordningen i vilken vektorerna tas också roll,

Direkt från definitionen följer det också att för varje skalär faktor k (tal) gäller följande:

Korsprodukten av kolinjära vektorer är lika med nollvektorn. Dessutom är korsprodukten av två vektorer noll om och endast om de är kolinjära. (Om en av dem är en nollvektor är det nödvändigt att komma ihåg att nollvektorn är kolinjär med vilken vektor som helst per definition).

Vector produkt har fördelningsegendom, det är

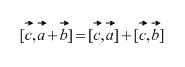
Uttrycket av korsprodukten i termer av vektorernas koordinater.

Låt två vektorer ges

(hur man hittar koordinaterna för en vektor genom koordinaterna för dess början och slut - se artikeln Prickprodukt av vektorer, stycke Alternativ definition av prickprodukten, eller beräkning av prickprodukten av två vektorer som ges av deras koordinater.)

Varför behöver du en vektorprodukt?

Det finns många sätt att använda korsprodukten, till exempel, som redan skrivits ovan, genom att beräkna korsprodukten av två vektorer, kan du ta reda på om de är kolinjära.

Eller det kan användas som ett sätt att beräkna arean av ett parallellogram byggt från dessa vektorer. Baserat på definitionen är längden på den resulterande vektorn området för detta parallellogram.

Också stor mängd applikationer finns inom elektricitet och magnetism.

Online-kalkylator för vektorprodukt.

För att hitta skalärprodukten av två vektorer med hjälp av denna kalkylator måste du ange koordinaterna för den första vektorn på första raden i ordningsföljd. andra - andra. Koordinaterna för vektorer kan beräknas från deras start- och slutkoordinater (se artikel Punktprodukt av vektorer , artikel En alternativ definition av punktprodukten, eller beräkning av punktprodukten av två vektorer givet deras koordinater.)