Վեկտորների վեկտորային արտադրյալ: Վեկտորների խառը արտադրյալ

Սահմանում. Վեկտորի a (բազմապատկիչ) վեկտորի արտադրյալը վեկտորի (բազմապատկիչի) կողմից, որը համակողմանի չէ դրան, երրորդ վեկտոր c (արտադրյալն է), որը կառուցված է հետևյալ կերպ.

1) դրա մոդուլը թվայինորեն հավասար է նկ. 155), որը կառուցված է վեկտորների վրա, այսինքն՝ հավասար է նշված զուգահեռագծի հարթությանը ուղղահայաց ուղղությանը.

3) այս դեպքում c վեկտորի ուղղությունը ընտրվում է (երկու հնարավորից), որպեսզի c վեկտորները կազմեն աջակողմյան համակարգ (§ 110):

Նշանակում՝ կամ

Սահմանման լրացում. Եթե ​​վեկտորները համագիծ են, ապա պատկերը դիտարկելով որպես (պայմանականորեն) զուգահեռագիծ, բնական է զրոյական տարածք վերագրելը: Հետևաբար, համագիծ վեկտորների վեկտորային արտադրյալը համարվում է հավասար զրոյական վեկտորին։

Քանի որ զրոյական վեկտորին կարող է վերագրվել ցանկացած ուղղություն, այս կոնվենցիան չի հակասում սահմանման 2-րդ և 3-րդ կետերին:

Դիտողություն 1. «Վեկտորային արտադրյալ» տերմինում առաջին բառը ցույց է տալիս, որ գործողության արդյունքը վեկտոր է (ի տարբերություն սկալյար արտադրյալի, տե՛ս § 104, դիտողություն 1):

Օրինակ 1. Գտե՛ք վեկտորային արտադրյալը, որտեղ աջ կոորդինատային համակարգի հիմնական վեկտորները (նկ. 156):

1. Քանի որ հիմնական վեկտորների երկարությունները հավասար են սանդղակի միավորին, զուգահեռագծի (քառակուսու) մակերեսը թվայինորեն հավասար է մեկի: Այսպիսով, վեկտորի արտադրյալի մոդուլը հավասար է մեկի:

2. Քանի որ հարթությանը ուղղահայացը առանցքն է, ցանկալի վեկտորային արտադրյալը վեկտոր է, որը համագիծ է k վեկտորին; և քանի որ երկուսն էլ ունեն մոդուլ 1, անհրաժեշտ խաչաձև արտադրյալը կա՛մ k է, կա՛մ -k:

3. Այս երկու հնարավոր վեկտորներից պետք է ընտրել առաջինը, քանի որ k վեկտորները կազմում են աջ համակարգ (իսկ վեկտորները՝ ձախ)։

Օրինակ 2. Գտե՛ք խաչաձև արտադրյալը

Լուծում. Ինչպես օրինակ 1-ում, մենք եզրակացնում ենք, որ վեկտորը կա՛մ k է, կա՛մ -k: Բայց հիմա մենք պետք է ընտրենք -k, քանի որ վեկտորները կազմում են ճիշտ համակարգը (իսկ վեկտորները կազմում են ձախը): Այսպիսով,

Օրինակ 3 Վեկտորներն ունեն համապատասխանաբար 80 և 50 սմ երկարություն և կազմում են 30° անկյուն: Ընդունելով մետրը որպես երկարության միավոր՝ գտե՛ք վեկտորի արտադրյալի երկարությունը a

Լուծում. Վեկտորների վրա կառուցված զուգահեռագծի մակերեսը հավասար է ցանկալի վեկտորի արտադրյալի երկարությունը հավասար է

Օրինակ 4. Գտե՛ք նույն վեկտորների խաչաձեւ արտադրյալի երկարությունը՝ որպես երկարության միավոր վերցնելով սանտիմետրը:

Լուծում. Քանի որ վեկտորների վրա կառուցված զուգահեռագծի մակերեսը հավասար է վեկտորի արտադրյալի երկարությանը, 2000 սմ է, այսինքն.

3 և 4 օրինակների համեմատությունը ցույց է տալիս, որ վեկտորի երկարությունը կախված է ոչ միայն գործոնների երկարությունից, այլև երկարության միավորի ընտրությունից։

Վեկտորային արտադրանքի ֆիզիկական նշանակությունը:Վեկտորային արտադրյալով ներկայացված բազմաթիվ ֆիզիկական մեծություններից մենք կդիտարկենք միայն ուժի պահը:

Թող A լինի ուժի կիրառման կետը: O կետի նկատմամբ ուժի պահը կոչվում է վեկտորային արտադրյալ: Քանի որ այս վեկտորային արտադրյալի մոդուլը թվայինորեն հավասար է զուգահեռագծի մակերեսին (Նկար 157), պահի մոդուլը հավասար է բազայի արտադրյալին բարձրությամբ, այսինքն՝ ուժը բազմապատկված է O կետից դեպի ուղիղ գիծ հեռավորության վրա, որի երկայնքով գործում է ուժը։

Մեխանիկայի մեջ ապացուցված է, որ կոշտ մարմնի հավասարակշռության համար անհրաժեշտ է, որ ոչ միայն մարմնի վրա կիրառվող ուժերը ներկայացնող վեկտորների գումարը, այլև ուժերի մոմենտների գումարը հավասար լինի զրոյի։ Այն դեպքում, երբ բոլոր ուժերը զուգահեռ են նույն հարթությանը, մոմենտները ներկայացնող վեկտորների գումարումը կարող է փոխարինվել դրանց մոդուլների գումարմամբ և հանելով։ Բայց ուժերի կամայական ուղղությունների համար նման փոխարինումն անհնար է։ Ըստ այդմ՝ խաչաձև արտադրյալը սահմանվում է հենց որպես վեկտոր, այլ ոչ թե որպես թիվ։

ԵՐԵՔ ՎԵԿՏՈՐՆԵՐԻ ԵՎ ՆՐԱ ՀԱՏԿՈՒԹՅՈՒՆՆԵՐԻ ԽԱՌՆ ԱՐՏԱԴՐԱՆՔ

խառը արտադրանքերեք վեկտոր կոչվում է այն թիվը, որը հավասար է . Նշվում է . Այստեղ առաջին երկու վեկտորները բազմապատկվում են վեկտորորեն, իսկ հետո ստացված վեկտորը սկալյար կերպով բազմապատկվում է երրորդ վեկտորով: Ակնհայտ է, որ նման ապրանքը որոշակի թիվ է:

Դիտարկենք խառը արտադրանքի հատկությունները:

1. երկրաչափական իմաստխառը արտադրանք. խառը արտադրանք 3 վեկտոր, մինչև մի նշան, հավասար է այս վեկտորների վրա կառուցված զուգահեռականի ծավալին, ինչպես եզրերի վրա, այսինքն. .

   Այսպիսով, և .

   

   Ապացույց. Եկեք հետաձգենք ընդհանուր ծագման վեկտորները և դրանց վրա կառուցենք զուգահեռականություն։ Նշենք և նշենք, որ. Ըստ սահմանման կետային արտադրանք

   Ենթադրելով դա և նշելով միջոցով հզուգահեռականի բարձրությունը, մենք գտնում ենք.

   Այսպիսով, ժամը

   Եթե ​​, ապա եւ . Հետևաբար, .

   Այս երկու դեպքերն էլ համադրելով՝ ստանում ենք կամ .

   Այս հատկության ապացույցից, մասնավորապես, հետևում է, որ եթե վեկտորների եռապատիկը ճիշտ է, ապա խառը արտադրյալը, իսկ եթե այն մնացել է, ապա .

2. Ցանկացած վեկտորների համար , հավասարությունը

   Այս հատկության ապացույցը բխում է սեփականությունից 1. Իրոք, հեշտ է ցույց տալ, որ և . Ընդ որում, «+» և «-» նշանները վերցվում են միաժամանակ, քանի որ վեկտորների և և և-ի միջև անկյունները երկուսն էլ սուր են կամ բութ:

3. Երբ ցանկացած երկու գործոն փոխվում է, խառը արտադրանքը փոխում է նշանը:

   Իսկապես, եթե հաշվի առնենք խառը արտադրանքը, ապա, օրինակ, կամ

4. Խառը արտադրյալ, եթե և միայն այն դեպքում, երբ գործոններից մեկը հավասար է զրոյի կամ վեկտորները համահարթակ են:

   Ապացույց.

   Այսպիսով, 3 վեկտորների համադրելիության անհրաժեշտ և բավարար պայման է նրանց խառը արտադրյալի հավասարությունը զրոյին։ Բացի այդ, սրանից հետևում է, որ երեք վեկտորները հիմք են կազմում տարածության մեջ, եթե .

   Եթե ​​վեկտորները տրված են կոորդինատային ձևով, ապա կարելի է ցույց տալ, որ դրանց խառը արտադրյալը գտնվել է բանաձևով.

   .

   Այսպիսով, խառը արտադրյալը հավասար է երրորդ կարգի որոշիչի, որի առաջին տողը պարունակում է առաջին վեկտորի կոորդինատները, երկրորդ տողը պարունակում է երկրորդ վեկտորի կոորդինատները, իսկ երրորդ տողը պարունակում է երրորդ վեկտորի կոորդինատները։

   Օրինակներ.

ՎԵՐԼՈՒԾԱԿԱՆ ԵՐԿՐԱՉԱՓՈՒԹՅՈՒՆԸ ՏԻԵԶԵՐՈՒԹՅԱՆ ՄԵՋ

Հավասարումը F (x, y, z)= 0-ը սահմանում է տարածության մեջ Օքսիզորոշ մակերես, այսինքն. կետերի վայր, որոնց կոորդինատները x, y, zբավարարել այս հավասարումը. Այս հավասարումը կոչվում է մակերեսային հավասարում և x, y, z- ընթացիկ կոորդինատները:

Այնուամենայնիվ, հաճախ մակերեսը սահմանվում է ոչ թե հավասարմամբ, այլ որպես տարածության կետերի մի շարք, որոնք ունեն այս կամ այն ​​հատկությունը: Այս դեպքում պահանջվում է գտնել մակերեսի հավասարումը` ելնելով նրա երկրաչափական հատկություններից:

ԻՆՔՆԱԹԻՌ.

ՆՈՐՄԱԼ ՊԼԱՆԻ ՎԵԿՏՈՐ.

ՏՐՎԱԾ ԿԵՏՈՎ ԱՆՑՆՈՂ ԻՆՔՆԱԹԻՐԻ ՀԱՎԱՍԱՐՈՒՄԸ

Դիտարկենք կամայական σ հարթություն տարածության մեջ: Նրա դիրքը որոշվում է այս հարթությանը ուղղահայաց վեկտոր և որոշ ֆիքսված կետ դնելով M0(x0, y 0, z0) ինքնաթիռում պառկած σ.

Ս հարթությանը ուղղահայաց վեկտորը կոչվում է նորմալայս հարթության վեկտորը: Թող վեկտորն ունենա կոորդինատներ:

Ստացվում է տվյալ կետով անցնող σ հարթության հավասարումը M0և ունենալով նորմալ վեկտոր: Դա անելու համար կամայական կետ վերցրեք σ հարթության վրա M(x, y, z)և հաշվի առեք վեկտորը:

Ցանկացած կետի համար ՄÎ σ վեկտոր։Ուստի նրանց սկալյար արտադրյալը հավասար է զրոյի։ Այս հավասարությունը պայմանն է, որ կետը ՄՕ ս. Այն գործում է այս հարթության բոլոր կետերի համար և խախտվում է հենց կետը Մկլինի ինքնաթիռից դուրս σ.

Եթե ​​շառավղով վեկտորով նշենք կետերը Մ, կետի շառավիղի վեկտորն է M0, ապա հավասարումը կարելի է գրել այսպես

Այս հավասարումը կոչվում է վեկտորհարթության հավասարումը. Գրենք կոորդինատային տեսքով։ Այդ ժամանակվանից

Այսպիսով, մենք ստացել ենք տվյալ կետով անցնող հարթության հավասարումը։ Այսպիսով, հարթության հավասարումը կազմելու համար անհրաժեշտ է իմանալ նորմալ վեկտորի կոորդինատները և հարթության վրա ընկած ինչ-որ կետի կոորդինատները։

Նշենք, որ հարթության հավասարումը 1-ին աստիճանի հավասարում է ընթացիկ կոորդինատների նկատմամբ. x, yև զ.

Օրինակներ.

ԻՆՔՆԱԹԻՐԻ ԸՆԴՀԱՆՈՒՐ ՀԱՎԱՍԱՐՈՒՄԸ

Կարելի է ցույց տալ, որ առաջին աստիճանի ցանկացած հավասարում դեկարտյան կոորդինատների նկատմամբ x, y, zինչ-որ հարթության հավասարում է: Այս հավասարումը գրված է այսպես.

Axe+By+Cz+D=0

և կանչեց ընդհանուր հավասարումհարթությունը և կոորդինատները A, B, Cահա հարթության նորմալ վեկտորի կոորդինատները.

Դիտարկենք ընդհանուր հավասարման առանձին դեպքեր: Եկեք պարզենք, թե ինչպես է հարթությունը գտնվում կոորդինատային համակարգի համեմատ, եթե հավասարման մեկ կամ մի քանի գործակիցներ անհետանում են:

A-ն առանցքի վրա հարթության կողմից կտրված հատվածի երկարությունն է Եզ. Նմանապես, կարելի է դա ցույց տալ բև գառանցքների վրա դիտարկված հարթությամբ կտրված հատվածների երկարություններն են Օյև Օզ.

Հարմար է հարթությունների կառուցման համար օգտագործել հարթության հավասարումը հատվածներում։

Այս առցանց հաշվիչը հաշվարկում է վեկտորների խաչաձև արտադրյալը: Մանրամասն լուծում է տրված։ Վեկտորների խաչաձև արտադրյալը հաշվարկելու համար մուտքագրեք վեկտորների կոորդինատները բջիջներում և սեղմեք «Հաշվարկել»:

×

Զգուշացում

Մաքրե՞լ բոլոր բջիջները:

Փակել Մաքրել

Տվյալների մուտքագրման հրահանգ.Թվերը մուտքագրվում են որպես ամբողջ թվեր (օրինակ՝ 487, 5, -7623 և այլն), տասնորդական թվեր (օրինակ՝ 67., 102.54 և այլն) կամ կոտորակներ։ Կոտորակը պետք է մուտքագրվի a/b ձևով, որտեղ a և b (b>0) ամբողջ կամ տասնորդական թվեր են: Օրինակներ 45/5, 6.6/76.4, -7/6.7 և այլն:

Վեկտորների խաչաձև արտադրյալ

Նախքան վեկտորների վեկտորային արտադրյալի սահմանմանը անցնելը, հաշվի առեք հասկացությունները պատվիրված վեկտորների եռակի, վեկտորների ձախ եռակի, վեկտորների աջ եռակի.

Սահմանում 1. Կանչվում են երեք վեկտորներ պատվիրել է եռակի(կամ եռակի), եթե նշված է, թե այս վեկտորներից որն է առաջինը, որը երկրորդը և որը երրորդը։

Ձայնագրությունը ԿԲԱ- նշանակում է - առաջինը վեկտոր է գ, երկրորդը վեկտորն է բիսկ երրորդը վեկտորն է ա.

Սահմանում 2. Ոչ համակողմանի վեկտորների եռակի աբգկոչվում է աջ (ձախ), եթե, երբ կրճատվում է ընդհանուր սկզբի վրա, այս վեկտորները դասավորված են այնպես, ինչպես համապատասխանաբար տեղակայված են աջ (ձախ) ձեռքի մեծ, չկռացած ցուցամատերը և միջին մատները:

Սահմանում 2-ը կարելի է ձևակերպել այլ կերպ.

Սահմանում 2. Ոչ համակողմանի վեկտորների եռակի աբգկոչվում է աջ (ձախ), եթե ընդհանուր սկզբնավորման դեպքում վեկտորը գգտնվում է վեկտորներով սահմանված հարթության մյուս կողմում աև բ, որտեղից ամենակարճ շրջադարձը ադեպի բկատարվում է հակառակ ուղղությամբ (ժամացույցի սլաքի ուղղությամբ):

Վեկտորային եռյակ աբգցույց է տրված նկ. 1-ը ճիշտ է և եռակի աբգցույց է տրված նկ. Մնացել է 2.

Եթե ​​վեկտորների երկու եռակի աջ կամ ձախ են, ապա ասում են, որ նրանք ունեն նույն կողմնորոշումը: Հակառակ դեպքում, ասում են, որ նրանք հակառակ կողմնորոշման են:

Սահմանում 3. Դեկարտյան կամ աֆինային կոորդինատային համակարգը կոչվում է աջ (ձախ), եթե երեք հիմնական վեկտորները կազմում են աջ (ձախ) եռապատիկ:

Հստակության համար մենք կքննարկենք միայն աջակողմյան կոորդինատային համակարգերը:

Սահմանում 4. վեկտորային արվեստվեկտոր ամեկ վեկտորի համար բկոչվում է վեկտոր Հետ, որը նշվում է խորհրդանիշով գ=[աբ] (կամ գ=[ա, բ], կամ c=a×b) և բավարարում է հետևյալ երեք պահանջները.

• վեկտորի երկարությունը Հետհավասար է վեկտորների երկարությունների արտադրյալին աև բանկյան սինուսին φ նրանց միջեւ:

|գ|=|[աբ]|=|ա||բ|sinφ;

(1)

• վեկտոր Հետուղղանկյուն վեկտորներից յուրաքանչյուրին աև բ;
• վեկտոր գուղղված այնպես, որ երեքը աբգճիշտ է.

Վեկտորների խաչաձև արտադրյալն ունի հետևյալ հատկությունները.

• [աբ]=−[բա] (հակափոփոխականությունգործոններ);
• [(λa)բ]=λ [աբ] (համատեղելիությունթվային գործոնի համեմատ);
• [(ա+բ)գ]=[ագ]+[բգ] (բաշխումվեկտորների գումարի համեմատ);
• [աա]=0 ցանկացած վեկտորի համար ա.

Վեկտորների խաչաձեւ արտադրյալի երկրաչափական հատկությունները

Թեորեմ 1. Որպեսզի երկու վեկտորները լինեն համագիծ, անհրաժեշտ և բավարար է, որ դրանց վեկտորային արտադրյալը հավասար լինի զրոյի:

Ապացույց. Անհրաժեշտություն. Թող վեկտորները աև բհամագիծ. Ապա նրանց միջև անկյունը 0 կամ 180° է և sinφ=մեղք180=մեղք 0=0. Հետևաբար, հաշվի առնելով (1) արտահայտությունը, վեկտորի երկարությունը գհավասար է զրոյի: Հետո գզրոյական վեկտոր.

Համարժեքություն. Թող վեկտորների խաչաձև արտադրյալը աև բնավարկել զրոյի: [ աբ]=0. Ապացուցենք, որ վեկտորները աև բհամագիծ. Եթե ​​վեկտորներից գոնե մեկը աև բզրո, ապա այս վեկտորները համագիծ են (քանի որ զրոյական վեկտորն ունի անորոշ ուղղություն և կարող է համարվել ցանկացած վեկտորի համագիծ):

Եթե ​​երկու վեկտորները աև բոչ զրոյական, ապա | ա|>0, |բ|>0. Այնուհետև [ աբ]=0 և (1)-ից հետևում է, որ sinφ=0. Այստեղից էլ վեկտորները աև բհամագիծ.

Թեորեմն ապացուցված է.

Թեորեմ 2. Վեկտորի արտադրյալի երկարությունը (մոդուլը) [ աբ] հավասար է մակերեսին Սզուգահեռագիծ, որը կառուցված է ընդհանուր ծագման վեկտորների վրա աև բ.

Ապացույց. Ինչպես գիտեք, զուգահեռագծի մակերեսը հավասար է այս զուգահեռագծի հարակից կողմերի և նրանց միջև անկյան սինուսի արտադրյալին: Հետևաբար.

Այնուհետև այս վեկտորների խաչաձև արտադրյալն ունի ձև.

Ընդարձակելով որոշիչը առաջին շարքի տարրերի վրա՝ ստանում ենք վեկտորի տարրալուծումը a×bհիմք ես, ժ, կ, որը համարժեք է (3) բանաձևին։

Թեորեմ 3-ի ապացույց. Կազմե՛ք հիմքի վեկտորների բոլոր հնարավոր զույգերը ես, ժ, կև հաշվարկել դրանց վեկտորի արտադրյալը: Պետք է հաշվի առնել, որ հիմքի վեկտորները փոխադարձաբար ուղղանկյուն են, կազմում են աջ եռապատիկ և ունեն միավորի երկարություն (այլ կերպ ասած՝ կարելի է ենթադրել, որ. ես={1, 0, 0}, ժ={0, 1, 0}, կ=(0, 0, 1)): Այնուհետև մենք ունենք.

Վերջին հավասարությունից և հարաբերություններից (4) մենք ստանում ենք.

Կազմեք 3×3 մատրիցա, որի առաջին շարքը հիմքի վեկտորներն են ես, ժ, կ,իսկ մնացած տողերը լցված են վեկտորների տարրերով աև բ.

Նախքան վեկտորային արտադրյալ հասկացությունը տալը, անդրադառնանք a → , b → , c → վեկտորների դասավորված եռյակի կողմնորոշման հարցին եռաչափ տարածության մեջ։

Սկսելու համար մի կետից մի կողմ դնենք a → , b → , c → վեկտորները։ a → , b → , c → եռակի կողմնորոշումը աջ կամ ձախ է՝ կախված c → վեկտորի ուղղությունից։ Այն ուղղությունից, որով կատարվում է ամենակարճ պտույտը a → վեկտորի c → b → վեկտորի վերջից, կորոշվի a → , b → , c → եռակի ձևը։

Եթե ​​ամենակարճ պտույտը ժամացույցի սլաքի ուղղությամբ է, ապա a → , b → , c → վեկտորների եռապատիկը կոչվում է. ճիշտեթե ժամացույցի սլաքի ուղղությամբ - ձախ.

Այնուհետև վերցրեք երկու ոչ գծային վեկտոր a → և b →: Ապա հետաձգենք A B → = a → և A C → = b → վեկտորները A կետից: Եկեք կառուցենք A D → = c → վեկտորը, որը միաժամանակ ուղղահայաց է և՛ A B → , և՛ A C → : Այսպիսով, A D → = c → վեկտորը կառուցելիս մենք կարող ենք երկու բան անել՝ տալով նրան կամ մեկ ուղղություն, կամ հակառակը (տես նկարազարդումը):

a → , b → , c → վեկտորների դասավորված եռյակը կարող է լինել, ինչպես պարզեցինք, աջ կամ ձախ՝ կախված վեկտորի ուղղությունից։

Վերոնշյալից մենք կարող ենք ներկայացնել վեկտորային արտադրանքի սահմանումը: Այս սահմանումը տրված է եռաչափ տարածության ուղղանկյուն կոորդինատային համակարգում սահմանված երկու վեկտորների համար։

Սահմանում 1

a → և b → երկու վեկտորների վեկտորային արտադրյալը Մենք կանվանենք այնպիսի վեկտոր, որը տրված է եռաչափ տարածության ուղղանկյուն կոորդինատային համակարգում այնպես, որ.

• եթե a → և b → վեկտորները համագիծ են, ապա այն կլինի զրո;
• այն ուղղահայաց կլինի ինչպես a →​— վեկտորին, այնպես էլ b վեկտորին → այսինքն. ∠ a → c → = ∠ b → c → = π 2;
• դրա երկարությունը որոշվում է բանաձևով՝ c → = a → b → sin ∠ a → , b → ;
• a → , b → , c → վեկտորների եռյակն ունի նույն կողմնորոշումը, ինչ տրված կոորդինատային համակարգը։

a → և b → վեկտորների խաչաձև արտադրյալն ունի հետևյալ նշումը՝ a → × b →.

Արտադրանքի խաչաձև կոորդինատներ

Քանի որ ցանկացած վեկտոր կոորդինատային համակարգում ունի որոշակի կոորդինատներ, կարելի է ներկայացնել վեկտորային արտադրյալի երկրորդ սահմանումը, որը թույլ կտա վեկտորների տրված կոորդինատներից գտնել նրա կոորդինատները։

Սահմանում 2

Եռաչափ տարածության ուղղանկյուն կոորդինատային համակարգում երկու վեկտորների վեկտորային արտադրյալ a → = (a x ; a y ; a z) և b → = (b x ; b y ; b z) կանչել վեկտորը c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → , որտեղ i → , j → , k → կոորդինատային վեկտորներ են:

Վեկտորային արտադրյալը կարող է ներկայացվել որպես երրորդ կարգի քառակուսի մատրիցայի որոշիչ, որտեղ առաջին շարքը orta վեկտորներն են i → , j → , k → , երկրորդ շարքը պարունակում է a → վեկտորի կոորդինատները, իսկ երրորդը։ b → վեկտորի կոորդինատներն են տրված ուղղանկյուն կոորդինատային համակարգում, այս մատրիցային որոշիչն ունի հետևյալ տեսքը. c → = a → × b → = i → j → k → a x a y a z b x b y b z.

Ընդլայնելով այս որոշիչն առաջին շարքի տարրերի վրա՝ ստանում ենք հավասարություն՝ c → = a → × b → = i → j → k → a x a y a z b x b y b z = a y a z b y b z i → - a x a z b x b z j → + a x a y b x b =y a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →

Խաչի արտադրանքի հատկությունները

Հայտնի է, որ վեկտորի արտադրյալը կոորդինատներում ներկայացված է որպես c → = a → × b → = i → j → k → a x a y a z b x b y b z մատրիցի որոշիչ, ապա հիմքի վրա. մատրիցային որոշիչ հատկություններհետեւյալը վեկտորի արտադրանքի հատկությունները.

1. հակակոմուտատիվություն a → × b → = - b → × a →;
2. բաշխվածություն a (1) → + a (2) → × b = a (1) → × b → + a (2) → × b → կամ a → × b (1) → + b (2) → = a → × b (1) → + a → × b (2) → ;
3. ասոցիատիվություն λ a → × b → = λ a → × b → կամ a → × (λ b →) = λ a → × b → , որտեղ λ կամայական իրական թիվ է։

Այս հատկությունները բարդ ապացույցներ չունեն:

Օրինակ, մենք կարող ենք ապացուցել վեկտորային արտադրանքի հակակոմուտատիվության հատկությունը։

Հակակոմուտատիվության ապացույց

Ըստ սահմանման՝ a → × b → = i → j → k → a x a y a z b x b y b z and b → × a → = i → j → k → b x b y b z a x a y a z . Եվ եթե մատրիցայի երկու տողերը փոխվում են, ապա մատրիցայի որոշիչի արժեքը պետք է փոխվի հակառակը, հետևաբար, a → × b → = i → j → k → a x a y a z b x b y b z = - i → j → k → b x b y b z a x a y. - b → × a → , որը և ապացուցում է վեկտորի արտադրյալի հակակոմուտատիվությունը։

Վեկտորային արտադրանք - Օրինակներ և լուծումներ

Շատ դեպքերում կան երեք տեսակի առաջադրանքներ.

Առաջին տիպի խնդիրներում սովորաբար տրվում են երկու վեկտորների երկարությունները և նրանց միջև եղած անկյունը, սակայն անհրաժեշտ է գտնել խաչաձև արտադրյալի երկարությունը: Այս դեպքում օգտագործեք հետևյալ բանաձևը c → = a → b → sin ∠ a → , b →.

Օրինակ 1

Գտե՛ք a → և b → վեկտորների խաչաձև արտադրյալի երկարությունը, եթե հայտնի է a → = 3, b → = 5, ∠ a →, b → = π 4:

Լուծում

Օգտագործելով a → և b → վեկտորների արտադրյալի երկարության սահմանումը, լուծում ենք այս խնդիրը՝ a → × b → = a → b → sin ∠ a → , b → = 3 5 sin π 4 = 15 2 2. .

Պատասխան. 15 2 2 .

Երկրորդ տիպի առաջադրանքները կապ ունեն վեկտորների կոորդինատների հետ, պարունակում են վեկտորային արտադրյալ, դրա երկարությունը և այլն։ որոնվել է հայտնի կոորդինատների միջոցով տրված վեկտորներ a → = (a x; a y; a z) և b → = (b x; b y; b z) .

Այս տեսակի առաջադրանքների համար դուք կարող եք լուծել առաջադրանքների բազմաթիվ տարբերակներ: Օրինակ, ոչ թե a → և b → վեկտորների կոորդինատները, այլ դրանց ընդլայնումները ձևի կոորդինատային վեկտորներում. b → = b x i → + b y j → + b z k → և c → = a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k →, կամ a → և b → վեկտորները կարող են տրվել դրանց կոորդինատներով. մեկնարկային և ավարտական ​​կետերը.

Դիտարկենք հետևյալ օրինակները.

Օրինակ 2

Ուղղանկյուն կոորդինատային համակարգում դրված են երկու վեկտորներ a → = (2 ; 1 ; - 3) , b → = (0 ; - 1 ; 1) : Գտեք դրանց վեկտորային արտադրյալը:

Լուծում

Երկրորդ սահմանման համաձայն՝ տրված կոորդինատներում գտնում ենք երկու վեկտորների վեկտորային արտադրյալը՝ a → × b → = (a y b z - a z b y) i → + (a z b x - a x b z) j → + (a x b y - a y b x) k → = = (1 1 - (- 3) (- 1)) i → + ((- 3) 0 - 2 1) j → + (2 (- 1) - 1 0) k → = = - 2 i → - 2 j → - 2 կ → .

Եթե ​​վեկտորի արտադրյալը գրենք մատրիցային որոշիչի միջոցով, ապա այս օրինակի լուծումը հետևյալն է՝ a → × b → = i → j → k → a x a y a z b x b y b z = i → j → k → 2 1 - 3 0 - 1 1 =. - 2 i → - 2 j → - 2 k → .

Պատասխան. a → × b → = - 2 i → - 2 j → - 2 k →.

Օրինակ 3

Գտե՛ք i → - j → և i → + j → + k → վեկտորների խաչաձև արտադրյալի երկարությունը, որտեղ i → , j → , k → - ուղղանկյուն դեկեկյան կոորդինատային համակարգի օրտներ։

Լուծում

Նախ գտնենք տրված վեկտորի i → - j → × i → + j → + k → կոորդինատները տրված ուղղանկյուն կոորդինատային համակարգում։

Հայտնի է, որ i → - j → և i → + j → + k → վեկտորներն ունեն համապատասխանաբար (1 ; - 1 ; 0) և (1 ; 1 ; 1) կոորդինատներ։ Գտե՛ք վեկտորի արտադրյալի երկարությունը՝ օգտագործելով մատրիցային որոշիչը, այնուհետև մենք ունենք i → - j → × i → + j → + k → = i → j → k → 1 - 1 0 1 1 1 = - i → - j → + 2 k → .

Հետեւաբար, i → - j → × i → + j → + k → վեկտորային արտադրյալը տրված կոորդինատային համակարգում ունի կոորդինատներ (- 1 ; - 1 ; 2):

Մենք գտնում ենք վեկտորի արտադրյալի երկարությունը բանաձևով (տե՛ս վեկտորի երկարությունը գտնելու բաժինը). i → - j → × i → + j → + k → = - 1 2 + - 1 2 + 2 2 = 6 .

Պատասխան. i → - j → × i → + j → + k → = 6. .

Օրինակ 4

A (1, 0, 1), B (0, 2, 3), C (1, 4, 2) երեք կետերի կոորդինատները տրված են ուղղանկյուն դեկարտյան կոորդինատային համակարգում: Գտե՛ք միաժամանակ A B → և A C → մի քանի վեկտորներ:

Լուծում

A B → և A C → վեկտորները համապատասխանաբար ունեն հետևյալ կոորդինատները (- 1 ; 2 ; 2) և (0 ; 4 ; 1): Գտնելով A B → և A C → վեկտորների վեկտորային արտադրյալը, ակնհայտ է, որ այն ըստ սահմանման ուղղահայաց վեկտոր է և՛ A B →, և՛ A C → →, այսինքն՝ դա մեր խնդրի լուծումն է։ Գտեք այն A B → × A C → = i → j → k → - 1 2 2 0 4 1 = - 6 i → + j → - 4 k →:

Պատասխան. - 6 i → + j → - 4 k → . ուղղահայաց վեկտորներից մեկն է։

Երրորդ տիպի խնդիրները ուղղված են վեկտորների վեկտորային արտադրյալի հատկությունների օգտագործմանը: Որը կիրառելուց հետո կստանանք տվյալ խնդրի լուծումը։

Օրինակ 5

a → և b → վեկտորները ուղղահայաց են, իսկ երկարությունները՝ համապատասխանաբար 3 և 4։ Գտեք 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3 a → × a → խաչաձև արտադրյալի երկարությունը. + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →.

Լուծում

Վեկտորային արտադրյալի բաշխման հատկությամբ կարող ենք գրել 3 a → - b → × a → - 2 b → = 3 a → × a → - 2 b → + - b → × a → - 2 b → = = 3. a → × a → + 3 a → × - 2 b → + - b → × a → + - b → × - 2 b →

Ասոցիատիվության հատկությամբ վերջին արտահայտության մեջ հանում ենք վեկտորային արտադրյալների նշանից դուրս թվային գործակիցները՝ 3 a → × a → + 3 a → × - 2 b → + - b → × a → + - b → ×. - 2 b → = = 3 a → × a → + 3 (- 2) a → × b → + (- 1) b → × a → + (- 1) (- 2) b → × b → = = 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b →

a → × a → և b → × b → վեկտորային արտադրյալները հավասար են 0-ի, քանի որ a → × a → = a → a → sin 0 = 0 և b → × b → = b → b → sin 0 = 0, ապա 3 a → × a → - 6 a → × b → - b → × a → + 2 b → × b → = - 6 a → × b → - b → × a → . .

Վեկտորային արտադրյալի հակակոմուտատիվությունից հետեւում է - 6 a → × b → - b → × a → = - 6 a → × b → - (- 1) a → × b → = - 5 a → × b → . .

Օգտագործելով վեկտորի արտադրյալի հատկությունները, մենք ստանում ենք 3 · a → - b → × a → - 2 · b → = = - 5 · a → × b → հավասարությունը:

Ըստ պայմանի՝ a → և b → վեկտորները ուղղահայաց են, այսինքն՝ նրանց միջև անկյունը հավասար է π 2-ի։ Այժմ մնում է միայն գտնված արժեքները փոխարինել համապատասխան բանաձևերով՝ 3 a → - b → × a → - 2 b → = - 5 a → × b → = = 5 a → × b → = 5 a → b → sin (a →, b →) = 5 3 4 sin π 2 = 60:

Պատասխան. 3 a → - b → × a → - 2 b → = 60:

Վեկտորների խաչաձեւ արտադրյալի երկարությունը ըստ սահմանման a → × b → = a → · b → · sin ∠ a → , b → . Քանի որ արդեն հայտնի է (դպրոցական դասընթացից), որ եռանկյան մակերեսը հավասար է նրա երկու կողմերի երկարությունների արտադրյալի կեսին՝ բազմապատկված այս կողմերի միջև անկյան սինուսով։ Հետևաբար, վեկտորի արտադրյալի երկարությունը հավասար է զուգահեռագծի մակերեսին՝ կրկնապատկված եռանկյունին, այն է՝ կողմերի արտադրյալը a → և b → վեկտորների տեսքով, որոնք անջատված են մեկ կետից, սինուսով։ նրանց միջև անկյան sin ∠ a → , b → .

Սա վեկտորային արտադրանքի երկրաչափական նշանակությունն է:

Վեկտորային արտադրանքի ֆիզիկական նշանակությունը

Մեխանիկայում՝ ֆիզիկայի ճյուղերից մեկը, վեկտորային արտադրյալի շնորհիվ կարող եք որոշել ուժի պահը տարածության կետի նկատմամբ։

Սահմանում 3

B կետի վրա կիրառված F → ուժի պահի տակ, A կետի նկատմամբ մենք կհասկանանք հետևյալ վեկտորային արտադրյալը A B → × F →.

Եթե ​​տեքստում սխալ եք նկատել, ընդգծեք այն և սեղմեք Ctrl+Enter

Ակնհայտ է, որ խաչաձև արտադրյալի դեպքում կարևոր է վեկտորների վերցման հերթականությունը, ավելին.

Նաև ուղղակիորեն սահմանումից հետևում է, որ ցանկացած սկալյար գործոնի k (թիվ) համար ճիշտ է հետևյալը.

Գոլգծային վեկտորների խաչաձև արտադրյալը հավասար է զրոյական վեկտորի: Ավելին, երկու վեկտորների խաչաձև արտադրյալը զրո է, եթե և միայն այն դեպքում, եթե դրանք համագիծ են: (Այն դեպքում, երբ դրանցից մեկը զրոյական վեկտոր է, անհրաժեշտ է հիշել, որ զրոյական վեկտորը ըստ սահմանման համագիծ է ցանկացած վեկտորի հետ):

Վեկտորային արտադրանքն ունի բաշխիչ սեփականություն, այն է

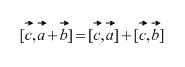
Խաչաձև արտադրյալի արտահայտությունը վեկտորների կոորդինատներով:

Թող տրվի երկու վեկտոր

(ինչպես գտնել վեկտորի կոորդինատները նրա սկզբի և վերջի կոորդինատներով. տե՛ս վեկտորների կետային արտադրյալ հոդվածը, պարբերություն Կետային արտադրյալի այլընտրանքային սահմանում կամ երկու վեկտորների կետային արտադրյալի հաշվարկ՝ տրված նրանց կոորդինատներով):

Ինչու՞ է ձեզ անհրաժեշտ վեկտորային արտադրանք:

Խաչաձև արտադրյալն օգտագործելու բազմաթիվ եղանակներ կան, օրինակ, ինչպես արդեն գրվել է վերևում, երկու վեկտորների խաչաձև արտադրյալը հաշվարկելով, կարող եք պարզել, թե արդյոք դրանք համագիծ են:

Կամ այն ​​կարող է օգտագործվել որպես այս վեկտորներից կառուցված զուգահեռագծի տարածքը հաշվարկելու միջոց: Սահմանման հիման վրա ստացված վեկտորի երկարությունը այս զուգահեռագծի տարածքն է:

Նաև մեծ գումարկիրառություններ կան էլեկտրականության և մագնիսականության մեջ:

Վեկտորային արտադրանքի առցանց հաշվիչ:

Այս հաշվիչը օգտագործելով երկու վեկտորների սկալյար արտադրյալը գտնելու համար անհրաժեշտ է առաջին տողում մուտքագրել առաջին վեկտորի կոորդինատները. երկրորդ - երկրորդ. Վեկտորների կոորդինատները կարող են հաշվարկվել սկզբի և վերջի կոորդինատներից (տես հոդված Վեկտորների կետային արտադրյալ , կետ Կետային արտադրյալի այլընտրանքային սահմանում կամ երկու վեկտորների կետային արտադրյալի հաշվարկ՝ հաշվի առնելով դրանց կոորդինատները:)